| 释义 |
Feigenbaum ConstantA universal constant for functions approaching Chaos via period doubling. It was discovered by Feigenbaum in 1975and demonstrated rigorously by Lanford (1982) and Collet and Eckmann (1979, 1980). The Feigenbaum constant 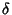 characterizes the geometric approach of the bifurcation parameter to its limiting value. Let characterizes the geometric approach of the bifurcation parameter to its limiting value. Let 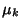 be the point atwhich a period be the point atwhich a period 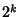 cycle becomes unstable. Denote the converged value by cycle becomes unstable. Denote the converged value by 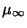 . Assuming geometric convergence,the difference between this value and . Assuming geometric convergence,the difference between this value and 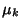 is denoted is denoted
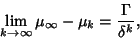 | (1) |
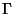 is a constant and is a constant and 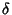 is a constant is a constant  . Solving for . Solving for 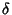 gives gives
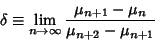 | (2) |
Amazingly, the Feigenbaum constant 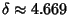 is ``universal'' (i.e., the same) for all 1-DMaps is ``universal'' (i.e., the same) for all 1-DMaps  if if  has a single locally quadratic Maximum. More specifically, the Feigenbaumconstant is universal for 1-D Maps if the Schwarzian Derivative has a single locally quadratic Maximum. More specifically, the Feigenbaumconstant is universal for 1-D Maps if the Schwarzian Derivative
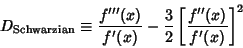 | (6) |
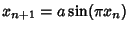 . The value of the Feigenbaum constant can be computed explicitly using functional grouprenormalization theory. The universal constant also occurs in phase transitions in physics and, curiously,is very nearly equal to . The value of the Feigenbaum constant can be computed explicitly using functional grouprenormalization theory. The universal constant also occurs in phase transitions in physics and, curiously,is very nearly equal to
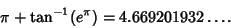 | (7) |
The Circle Map is not universal, and has a Feigenbaum constant of 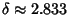 .For an Area-Preserving 2-D Map with .For an Area-Preserving 2-D Map with
the Feigenbaum constant is 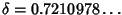 (Tabor 1989, p. 225). For a function of the form (Tabor 1989, p. 225). For a function of the form
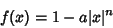 | (10) |
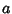 and and 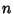 constant and constant and 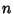 an Integer, the Feigenbaum constant for various an Integer, the Feigenbaum constant for various 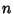 is given in the following table (Briggs 1991, Briggs et al. 1991), which updates the values in Tabor (1989, p. 225). is given in the following table (Briggs 1991, Briggs et al. 1991), which updates the values in Tabor (1989, p. 225).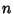 | 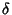 | | 2 | 5.9679 | | 4 | 7.2846 | | 6 | 8.3494 | | 8 | 9.2962 |
An additional constant  , defined as the separation of adjacent elements of Period Doubled Attractors from one double to the next, has a value , defined as the separation of adjacent elements of Period Doubled Attractors from one double to the next, has a value
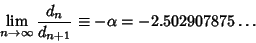 | (11) |
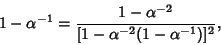 | (12) |
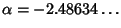 , only 0.7% off from theactual value (Feigenbaum 1988).See also Attractor, Bifurcation,Feigenbaum Function, Linear Stability, Logistic Map, Period Doubling , only 0.7% off from theactual value (Feigenbaum 1988).See also Attractor, Bifurcation,Feigenbaum Function, Linear Stability, Logistic Map, Period Doubling
References
Briggs, K. ``A Precise Calculation of the Feigenbaum Constants.'' Math. Comput. 57, 435-439, 1991.Briggs, K.; Quispel, G.; and Thompson, C. ``Feigenvalues for Mandelsets.'' J. Phys. A: Math. Gen. 24 3363-3368, 1991. Briggs, K.; Quispel, G.; and Thompson, C. ``Feigenvalues for Mandelsets.'' http://epidem13.plantsci.cam.ac.uk/~kbriggs/. Collet, P. and Eckmann, J.-P. ``Properties of Continuous Maps of the Interval to Itself.'' Mathematical Problems in Theoretical Physics (Ed. K. Osterwalder). New York: Springer-Verlag, 1979. Collet, P. and Eckmann, J.-P. Iterated Maps on the Interval as Dynamical Systems. Boston, MA: Birkhäuser, 1980. Eckmann, J.-P. and Wittwer, P. Computer Methods and Borel Summability Applied to Feigenbaum's Equations. New York: Springer-Verlag, 1985. Feigenbaum, M. J. ``Presentation Functions, Fixed Points, and a Theory of Scaling Function Dynamics.'' J. Stat. Phys. 52, 527-569, 1988. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/fgnbaum/fgnbaum.html Finch, S. ``Generalized Feigenbaum Constants.'' http://www.mathsoft.com/asolve/constant/fgnbaum/general.html. Lanford, O. E. ``A Computer-Assisted Proof of the Feigenbaum Conjectures.'' Bull. Amer. Math. Soc. 6, 427-434, 1982. Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, 1990. Stephenson, J. W. and Wang, Y. ``Numerical Solution of Feigenbaum's Equation.'' Appl. Math. Notes 15, 68-78, 1990. Stephenson, J. W. and Wang, Y. ``Relationships Between the Solutions of Feigenbaum's Equations.'' Appl. Math. Let. 4, 37-39, 1991. Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.
|
![]() characterizes the geometric approach of the bifurcation parameter to its limiting value. Let
characterizes the geometric approach of the bifurcation parameter to its limiting value. Let ![]() be the point atwhich a period
be the point atwhich a period ![]() cycle becomes unstable. Denote the converged value by
cycle becomes unstable. Denote the converged value by ![]() . Assuming geometric convergence,the difference between this value and
. Assuming geometric convergence,the difference between this value and ![]() is denoted
is denoted![]() is ``universal'' (i.e., the same) for all 1-DMaps
is ``universal'' (i.e., the same) for all 1-DMaps ![]() if
if ![]() has a single locally quadratic Maximum. More specifically, the Feigenbaumconstant is universal for 1-D Maps if the Schwarzian Derivative
has a single locally quadratic Maximum. More specifically, the Feigenbaumconstant is universal for 1-D Maps if the Schwarzian Derivative![]() .For an Area-Preserving 2-D Map with
.For an Area-Preserving 2-D Map with![]() , defined as the separation of adjacent elements of Period Doubled Attractors from one double to the next, has a value
, defined as the separation of adjacent elements of Period Doubled Attractors from one double to the next, has a value