| 释义 |
Fermat's Little TheoremIf 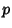 is a Prime number and is a Prime number and 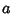 a Natural Number, then a Natural Number, then
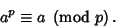 | (1) |
 ( (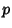 does not divide does not divide 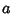 ), then there exists some smallest exponent ), then there exists some smallest exponent  such that such that
 | (2) |
 divides divides  . Hence, . Hence,
 | (3) |
 the first proof waspublished by Euler the first proof waspublished by Euler  in 1749. in 1749.
The theorem is easily proved using mathematical Induction. Suppose  . Then examine . Then examine
 | (4) |
 | (5) |
 | (6) |
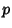 divides the right side, so it also divides the left side. Combining with the induction hypothesis gives that divides the right side, so it also divides the left side. Combining with the induction hypothesis gives that 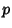 divides the sum divides the sum
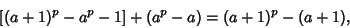 | (7) |
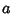 . The theorem is sometimes called Fermat's Simple Theorem.Wilson's Theorem follows as a Corollary of Fermat's Little Theorem. . The theorem is sometimes called Fermat's Simple Theorem.Wilson's Theorem follows as a Corollary of Fermat's Little Theorem.
Fermat's little theorem shows that, if 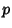 is Prime, there does not exist a base is Prime, there does not exist a base  with with  such that such that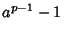 possesses a nonzero residue modulo possesses a nonzero residue modulo 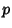 . If such base . If such base 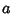 exists, exists, 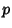 is therefore guaranteed to be composite.However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that is therefore guaranteed to be composite.However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that 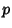 is Prime. The propertyof unambiguously certifying composite numbers while passing some Primes make Fermat's little theorem a CompositenessTest which is sometimes called the Fermat Compositeness Test. Composite Numbers known asFermat Pseudoprimes (or sometimes simply ``Pseudoprimes'') have zeroresidue for some is Prime. The propertyof unambiguously certifying composite numbers while passing some Primes make Fermat's little theorem a CompositenessTest which is sometimes called the Fermat Compositeness Test. Composite Numbers known asFermat Pseudoprimes (or sometimes simply ``Pseudoprimes'') have zeroresidue for some 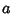 s and so are not identified as composite. Worse still, there exist numbers known as CarmichaelNumbers (the smallest of which is 561) which give zero residue for any choice of the base s and so are not identified as composite. Worse still, there exist numbers known as CarmichaelNumbers (the smallest of which is 561) which give zero residue for any choice of the base 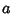 Relatively Prime to Relatively Prime to 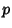 . However, Fermat's Little Theorem Converse provides a criterion for certifying theprimality of a number. . However, Fermat's Little Theorem Converse provides a criterion for certifying theprimality of a number.
A number satisfying Fermat's little theorem for some nontrivial base and which is not known to be composite is called aProbable Prime. A table of the smallest Pseudoprimes 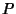 for the first 100 bases for the first 100 bases 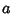 follows(Sloane's A007535). follows(Sloane's A007535).
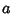 | 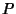 | 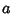 | 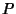 | 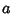 | 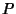 | 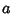 | 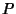 | 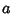 | 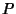 | | 2 | 341 | 22 | 69 | 42 | 205 | 62 | 63 | 82 | 91 | | 3 | 91 | 23 | 33 | 43 | 77 | 63 | 341 | 83 | 105 | | 4 | 15 | 24 | 25 | 44 | 45 | 64 | 65 | 84 | 85 | | 5 | 124 | 25 | 28 | 45 | 76 | 65 | 133 | 85 | 129 | | 6 | 35 | 26 | 27 | 46 | 133 | 66 | 91 | 86 | 87 | | 7 | 25 | 27 | 65 | 47 | 65 | 67 | 85 | 87 | 91 | | 8 | 9 | 28 | 87 | 48 | 49 | 68 | 69 | 88 | 91 | | 9 | 28 | 29 | 35 | 49 | 66 | 69 | 85 | 89 | 99 | | 10 | 33 | 30 | 49 | 50 | 51 | 70 | 169 | 90 | 91 | | 11 | 15 | 31 | 49 | 51 | 65 | 71 | 105 | 91 | 115 | | 12 | 65 | 32 | 33 | 52 | 85 | 72 | 85 | 92 | 93 | | 13 | 21 | 33 | 85 | 53 | 65 | 73 | 111 | 93 | 301 | | 14 | 15 | 34 | 35 | 54 | 55 | 74 | 75 | 94 | 95 | | 15 | 341 | 35 | 51 | 55 | 63 | 75 | 91 | 95 | 141 | | 16 | 51 | 36 | 91 | 56 | 57 | 76 | 77 | 96 | 133 | | 17 | 45 | 37 | 45 | 57 | 65 | 77 | 95 | 97 | 105 | | 18 | 25 | 38 | 39 | 58 | 95 | 78 | 341 | 98 | 99 | | 19 | 45 | 39 | 95 | 59 | 87 | 79 | 91 | 99 | 145 | | 20 | 21 | 40 | 91 | 60 | 341 | 80 | 81 | 100 | 259 | | 21 | 55 | 41 | 105 | 61 | 91 | 81 | 85 | | |
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 61, 1987.Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 141-142, 1996. Courant, R. and Robbins, H. ``Fermat's Theorem.'' §2.2 in Supplement to Ch. 1 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 37-38, 1996. Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 20, 1993. Sloane, N. J. A. SequenceA007535/M5440in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
![]() is a Prime number and
is a Prime number and ![]() a Natural Number, then
a Natural Number, then![]() . Then examine
. Then examine![]() is Prime, there does not exist a base
is Prime, there does not exist a base ![]() with
with ![]() such that
such that![]() possesses a nonzero residue modulo
possesses a nonzero residue modulo ![]() . If such base
. If such base ![]() exists,
exists, ![]() is therefore guaranteed to be composite.However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that
is therefore guaranteed to be composite.However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that ![]() is Prime. The propertyof unambiguously certifying composite numbers while passing some Primes make Fermat's little theorem a CompositenessTest which is sometimes called the Fermat Compositeness Test. Composite Numbers known asFermat Pseudoprimes (or sometimes simply ``Pseudoprimes'') have zeroresidue for some
is Prime. The propertyof unambiguously certifying composite numbers while passing some Primes make Fermat's little theorem a CompositenessTest which is sometimes called the Fermat Compositeness Test. Composite Numbers known asFermat Pseudoprimes (or sometimes simply ``Pseudoprimes'') have zeroresidue for some ![]() s and so are not identified as composite. Worse still, there exist numbers known as CarmichaelNumbers (the smallest of which is 561) which give zero residue for any choice of the base
s and so are not identified as composite. Worse still, there exist numbers known as CarmichaelNumbers (the smallest of which is 561) which give zero residue for any choice of the base ![]() Relatively Prime to
Relatively Prime to ![]() . However, Fermat's Little Theorem Converse provides a criterion for certifying theprimality of a number.
. However, Fermat's Little Theorem Converse provides a criterion for certifying theprimality of a number.![]() for the first 100 bases
for the first 100 bases ![]() follows(Sloane's A007535).
follows(Sloane's A007535).