Frobenius Method
If ![]() is an ordinary point of the Ordinary Differential Equation, expand
is an ordinary point of the Ordinary Differential Equation, expand ![]() in a Taylor Series about
in a Taylor Series about ![]() , letting
, letting
 | (1) |
 | (2) | ||
 | (3) | ||
 | |||
| (4) |
If
| (5) |
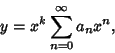 | (6) |
 | (7) | ||
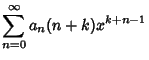 | (8) | ||
 | (9) |
Now, plug
Fuchs's Theorem guarantees that at least one Power series solution will be obtained when applying the Frobeniusmethod if the expansion point is an ordinary, or regular, Singular Point. For a regularSingular Point, a Laurent Series expansion can also be used. Expand ![]() in aLaurent Series, letting
in aLaurent Series, letting
| (10) |
References
Arfken, G. ``Series Solutions--Frobenius' Method.'' §8.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 454-467, 1985.
- Euler Power Conjecture
- Euler Product
- Euler Pseudoprime
- Euler Quartic Conjecture
- Euler's 6n+1 Theorem
- Euler's Addition Theorem
- Euler's Circle
- Euler's Conjecture
- Euler's Criterion
- Euler's Displacement Theorem
- Euler's Distribution Theorem
- Euler's Factorization Method
- Euler's Finite Difference Transformation
- Euler's Graeco-Roman Squares Conjecture
- Euler's Homogeneous Function Theorem
- Euler's Hypergeometric Transformations
- Euler's Idoneal Number
- Euler's Machin-Like Formula
- Euler's Pentagonal Number Theorem
- Euler's Phi Function
- Euler's Polygon Division Problem
- Euler's Quadratic Residue Theorem
- Euler Square
- Euler's Rotation Theorem
- Euler's Rule