| 释义 |
Gaussian Distribution Linear Combination of VariatesIf  is Normally Distributed with Mean is Normally Distributed with Mean 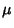 and Variance and Variance 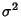 , thena linear function of , thena linear function of  , ,
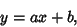 | (1) |
 andVariance andVariance  , as can be derived using the Moment-Generating Function , as can be derived using the Moment-Generating Function
which is of the standard form with
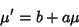 | (3) |
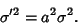 | (4) |
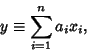 | (5) |
Setting this equal to
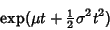 | (7) |
Therefore, the Mean and Variance of the weighted sums of  Random Variablesare their weighted sums. Random Variablesare their weighted sums.
If  are Independent and Normally Distributed with Mean 0 and Variance are Independent and Normally Distributed with Mean 0 and Variance 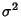 , define , define
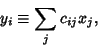 | (10) |
 obeys the Orthogonality Condition obeys the Orthogonality Condition
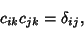 | (11) |
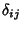 the Kronecker Delta. Then the Kronecker Delta. Then  are also independent and normally distributed with Mean 0and Variance are also independent and normally distributed with Mean 0and Variance 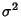 . . |
![]() is Normally Distributed with Mean
is Normally Distributed with Mean ![]() and Variance
and Variance ![]() , thena linear function of
, thena linear function of ![]() ,
,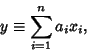
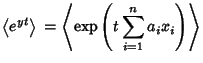
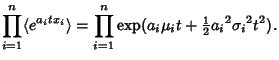
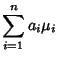
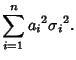
![]() are Independent and Normally Distributed with Mean 0 and Variance
are Independent and Normally Distributed with Mean 0 and Variance ![]() , define
, define