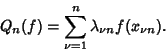| 释义 |
Gaussian QuadratureSeeks to obtain the best numerical estimate of an integral by picking optimal Abscissas  at whichto evaluate the function at whichto evaluate the function  . The Fundamental Theorem of Gaussian Quadrature states that the optimalAbscissas of the . The Fundamental Theorem of Gaussian Quadrature states that the optimalAbscissas of the  -point Gaussian Quadrature Formulas are precisely theroots of the orthogonal Polynomial for the same interval and Weighting Function. Gaussian quadrature is optimalbecause it fits all Polynomials up to degree -point Gaussian Quadrature Formulas are precisely theroots of the orthogonal Polynomial for the same interval and Weighting Function. Gaussian quadrature is optimalbecause it fits all Polynomials up to degree  exactly. Slightly less optimal fits are obtainedfrom Radau Quadrature and Laguerre Quadrature. exactly. Slightly less optimal fits are obtainedfrom Radau Quadrature and Laguerre Quadrature.
To determine the weights corresponding to the Gaussian Abscissas, compute a Lagrange InterpolatingPolynomial for  by letting by letting
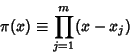 | (1) |
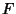 instead of instead of  ), so ), so
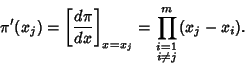 | (2) |
 points gives points gives
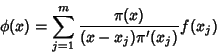 | (3) |
 . We are therefore looking for a set of points . We are therefore looking for a set of points 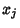 and weights and weights 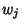 such that for aWeighting Function such that for aWeighting Function 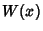 , ,
with Weight
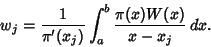 | (5) |
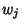 are sometimes also called the Christoffel Number (Chandrasekhar 1967).For orthogonal Polynomials are sometimes also called the Christoffel Number (Chandrasekhar 1967).For orthogonal Polynomials 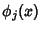 with with  =1, ..., =1, ...,  , ,
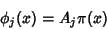 | (6) |
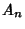 is the Coefficient of is the Coefficient of 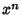 in in 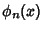 , then , then
where
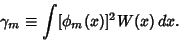 | (8) |
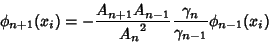 | (9) |
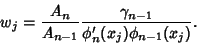 | (10) |
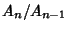 .) In Gaussian quadrature, the weights are allPositive. The error is given by .) In Gaussian quadrature, the weights are allPositive. The error is given by
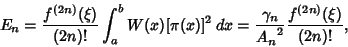 | (11) |
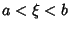 (Hildebrand 1956, pp. 320-321). (Hildebrand 1956, pp. 320-321).
Other curious identities are
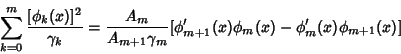 | (12) |
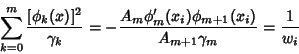 | (13) |
In the Notation of Szegö (1975), let 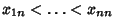 be an ordered set of points in be an ordered set of points in 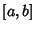 , and let , and let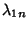 , ..., , ..., 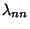 be a set of Real Numbers. If be a set of Real Numbers. If  is an arbitrary function on the Closed Interval is an arbitrary function on the Closed Interval 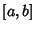 , writethe Mechanical Quadrature as , writethe Mechanical Quadrature as
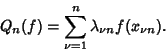 | (14) |
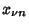 are the Abscissas and are the Abscissas and 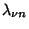 are the Cotes Numbers.See also Chebyshev Quadrature, Chebyshev-Gauss Quadrature, Chebyshev-Radau Quadrature, FundamentalTheorem of Gaussian Quadrature, Hermite-Gauss Quadrature, Jacobi-Gauss Quadrature, Laguerre-GaussQuadrature, Legendre-Gauss Quadrature, Lobatto Quadrature, Mehler Quadrature, Radau Quadrature are the Cotes Numbers.See also Chebyshev Quadrature, Chebyshev-Gauss Quadrature, Chebyshev-Radau Quadrature, FundamentalTheorem of Gaussian Quadrature, Hermite-Gauss Quadrature, Jacobi-Gauss Quadrature, Laguerre-GaussQuadrature, Legendre-Gauss Quadrature, Lobatto Quadrature, Mehler Quadrature, Radau Quadrature
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 887-888, 1972.Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 103, 1990. Arfken, G. ``Appendix 2: Gaussian Quadrature.'' Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 968-974, 1985. Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 461, 1987. Chandrasekhar, S. An Introduction to the Study of Stellar Structure. New York: Dover, 1967. Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 319-323, 1956. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gaussian Quadratures and Orthogonal Polynomials.'' §4.5 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 140-155, 1992. Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 37-48 and 340-349, 1975. Whittaker, E. T. and Robinson, G. The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 152-163, 1967. |
![]() at whichto evaluate the function
at whichto evaluate the function ![]() . The Fundamental Theorem of Gaussian Quadrature states that the optimalAbscissas of the
. The Fundamental Theorem of Gaussian Quadrature states that the optimalAbscissas of the ![]() -point Gaussian Quadrature Formulas are precisely theroots of the orthogonal Polynomial for the same interval and Weighting Function. Gaussian quadrature is optimalbecause it fits all Polynomials up to degree
-point Gaussian Quadrature Formulas are precisely theroots of the orthogonal Polynomial for the same interval and Weighting Function. Gaussian quadrature is optimalbecause it fits all Polynomials up to degree ![]() exactly. Slightly less optimal fits are obtainedfrom Radau Quadrature and Laguerre Quadrature.
exactly. Slightly less optimal fits are obtainedfrom Radau Quadrature and Laguerre Quadrature.![]() by letting
by letting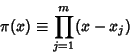
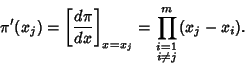
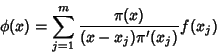
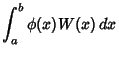
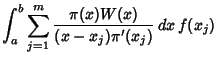
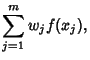
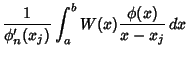
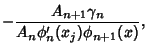
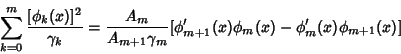
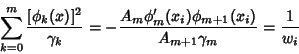
![]() be an ordered set of points in
be an ordered set of points in ![]() , and let
, and let![]() , ...,
, ..., ![]() be a set of Real Numbers. If
be a set of Real Numbers. If ![]() is an arbitrary function on the Closed Interval
is an arbitrary function on the Closed Interval ![]() , writethe Mechanical Quadrature as
, writethe Mechanical Quadrature as