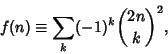| 释义 |
Generalized Hypergeometric FunctionThe generalized hypergeometric function is given by a Hypergeometric Series, i.e., a series for which the ratio of successive terms can be written
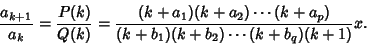 | (1) |
 in the Denominator is present for historical reasons of notation.)The resulting generalized hypergeometric function is written in the Denominator is present for historical reasons of notation.)The resulting generalized hypergeometric function is written
where 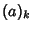 is the Pochhammer Symbol or Rising Factorial is the Pochhammer Symbol or Rising Factorial
 | (4) |
 , then the function is abbreviated , then the function is abbreviated
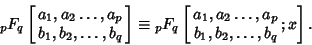 | (5) |
 is ``the'' Hypergeometric Function, and is ``the'' Hypergeometric Function, and 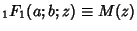 is the ConfluentHypergeometric Function. A function of the form is the ConfluentHypergeometric Function. A function of the form 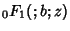 is called a Confluent Hypergeometric Limit Function. is called a Confluent Hypergeometric Limit Function.
The generalized hypergeometric function
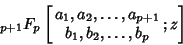 | (6) |
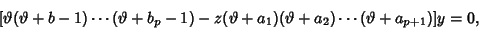 | (7) |
 | (8) |
 | (9) |
A generalized hypergeometric equation is termed ``well posed'' if
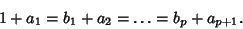 | (10) |
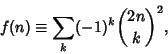 | (11) |
 | (12) |
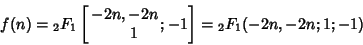 | (13) |
Gosper (1978) discovered a slew of unusual hypergeometric function identities, many of which were subsequently proven by Gesseland Stanton (1982). An important generalization of Gosper's technique, called Zeilberger's Algorithm, in turn led tothe powerful machinery of the Wilf-Zeilberger Pair (Zeilberger 1990).
Special hypergeometric identities include Gauss's Hypergeometric Theorem
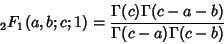 | (14) |
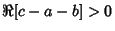 , Kummer's Formula , Kummer's Formula
 | (15) |
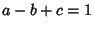 and and 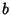 is a positive integer, Saalschütz's Theorem is a positive integer, Saalschütz's Theorem
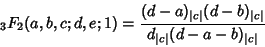 | (16) |
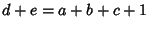 with with  a negative integer and a negative integer and  the Pochhammer Symbol, Dixon's Theorem the Pochhammer Symbol, Dixon's Theorem
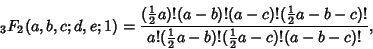 | (17) |
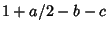 has a positive Real Part, has a positive Real Part, 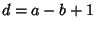 , and , and  , the Clausen Formula , the Clausen Formula
 | (18) |
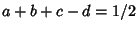 , , 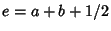 , , 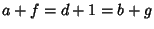 , ,  a nonpositive integer, and the Dougall-Ramanujan Identity a nonpositive integer, and the Dougall-Ramanujan Identity
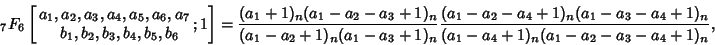 | (19) |
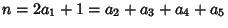 , , 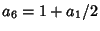 , , 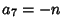 , and , and  for for  , 2, ..., 6. For all these identities, , 2, ..., 6. For all these identities, is the Pochhammer Symbol. is the Pochhammer Symbol.
Gessel (1994) found a slew of new identities using Wilf-Zeilberger Pairs, including the following:
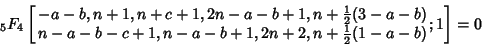 | (20) |
 | (21) |
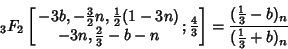 | (22) |
 | (23) |
References
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.Dwork, B. Generalized Hypergeometric Functions. Oxford, England: Clarendon Press, 1990. Exton, H. Multiple Hypergeometric Functions and Applications. New York: Wiley, 1976. Gessel, I. ``Finding Identities with the WZ Method.'' Theoret. Comput. Sci. To appear. Gessel, I. and Stanton, D. ``Strange Evaluations of Hypergeometric Series.'' SIAM J. Math. Anal. 13, 295-308, 1982. Gosper, R. W. ``Decision Procedures for Indefinite Hypergeometric Summation.'' Proc. Nat. Acad. Sci. USA 75, 40-42, 1978. Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, 1996. Saxena, R. K. and Mathai, A. M. Generalized Hypergeometric Functions with Applications in Statistics and Physical Sciences. New York: Springer-Verlag, 1973. Slater, L. J. Generalized Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1966. Zeilberger, D. ``A Fast Algorithm for Proving Terminating Hypergeometric Series Identities.'' Discrete Math. 80, 207-211, 1990. |


![]() is ``the'' Hypergeometric Function, and
is ``the'' Hypergeometric Function, and ![]() is the ConfluentHypergeometric Function. A function of the form
is the ConfluentHypergeometric Function. A function of the form ![]() is called a Confluent Hypergeometric Limit Function.
is called a Confluent Hypergeometric Limit Function.