Umbral Calculus
The study of certain properties of Sylvester 
from the word ``umbra'' (meaning ``shadow'' in Latin), and reflects the fact that for many types of identities involvingsequences of polynomials with Powers 
, ``shadow'' identities are obtained when the polynomials arechanged to discrete values and the exponent in is changed to the Pochhammer Symbol 
.
For example, Newton's Forward Difference Formula written in the form
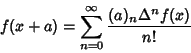 | (1) |
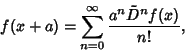looks suspiciously like a finite analog of the Taylor Series expansion | (2) |
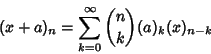is the Differential Operator. Similarly, the Chu-Vandermonde Identity | (3) |
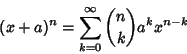a Binomial Coefficient, looks suspiciously like an analog of the Binomial Theorem | (4) |
References
Roman, S. and Rota, G.-C. ``The Umbral Calculus.'' Adv. Math. 27, 95-188, 1978. Roman, S. The Umbral Calculus. New York: Academic Press, 1984.
- Isovolume Problem
- Isthmus
- Iterated Exponential Constants
- Iterated Function System
- Iterated Radical
- Iteration Sequence
- Itô's Lemma
- Itô's Theorem
- Iverson Bracket
- Iwasawa's Theorem
- j
- Jackson's Difference Fan
- Jackson's Identity
- Jackson's Theorem
- Jacobi Algorithm
- Jacobian
- Jacobian Conjecture
- Jacobian Curve
- Jacobian Determinant
- Jacobi-Anger Expansion
- Jacobian Group
- Jacobi Differential Equation
- Jacobi Differential Equation (Calculus of Variations)
- Jacobi Elliptic Functions
- Jacobi Function of the First Kind