| 释义 |
Heat Conduction EquationA diffusion equation  of the form of the form
 | (1) |
 is the thermal diffusivity is the thermal diffusivity  and and  the temperature. the temperature. 
The 1-D heat conduction equation is
 | (2) |
 | (3) |
 | (4) |
 gives gives
 | (5) |
 , we have picked a negativeseparation constant so that the solution remains finite at all times and , we have picked a negativeseparation constant so that the solution remains finite at all times and  has units of length. The has units of length. The  solutionis solutionis
 | (6) |
 solution is solution is
 | (7) |
If we are given the boundary conditions
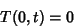 | (9) |
 | (10) |
 | (11) |
 | (12) |
 | (13) |
 , ,
 | (14) |
 , we have , we have
 | (15) |
 and integrating from 0 to and integrating from 0 to  gives gives
 | (16) |
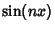 and and  , , | |  | (17) |
so
 | (18) |
If the boundary conditions are replaced by the requirement that the derivative of the temperature be zero at the edges,then (9) and (10) are replaced by
 | (19) |
 | (20) |
 | (21) |
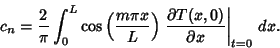 | (22) |
|
![]() of the form
of the form


