| 释义 |
Helmholtz Differential Equation--Conical CoordinatesIn Conical Coordinates, Laplace's Equation can be written
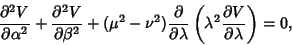 | (1) |
(Byerly 1959). Letting
 | (4) |
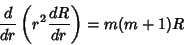 | (5) |
 | (6) |
 | (7) |
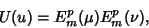 | (8) |
 are Ellipsoidal Harmonics. The regular solution is therefore are Ellipsoidal Harmonics. The regular solution is therefore
 | (9) |
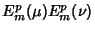 is an is an  th degree SphericalHarmonic. th degree SphericalHarmonic.
References
Arfken, G. ``Conical Coordinates 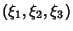 .'' §2.16 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 118-119, 1970. .'' §2.16 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 118-119, 1970.Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, p. 263, 1959. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 514 and 659, 1953.
|

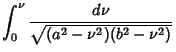
![]() .'' §2.16 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 118-119, 1970.
.'' §2.16 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 118-119, 1970.