Homothetic Center
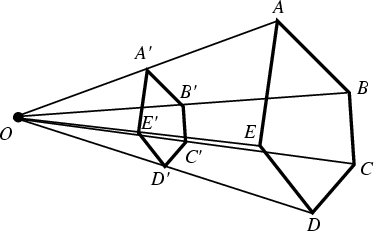
The meeting point of lines that connect corresponding points from Homothetic figures. In the above figure, 
isthe homothetic center of the Homothetic figures 
and 
. For figures which are similar but do nothave Parallel sides, a Similitude Center exists (Johnson 1929, pp. 16-20).
Given two nonconcentric Circles, draw Radii Parallel and in the samedirection. Then the line joining the extremities of the Radii passes through a fixed point on the line ofcenters which divides that line externally in the ratio of Radii. This point is called the externalhomothetic center, or external center of similitude (Johnson 1929, pp. 19-20 and 41).
If Radii are drawn Parallel but instead in opposite directions, the extremities of theRadii pass through a fixed point on the line of centers which divides that line internally in the ratio ofRadii (Johnson 1929, pp. 19-20 and 41). This point is called the internal homothetic center, or internalcenter of similitude (Johnson 1929, pp. 19-20 and 41).
The position of the homothetic centers for two circles of radii 
, centers 
, and segment angle 
are given by solving the simultaneous equations
 |  |  | |
 | |  |
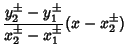for
, where |  |  | |
 | |  |
and the plus signs give the external homothetic center, while the minus signs give the internal homothetic center.
As the above diagrams show, as the angles of the parallel segments are varied, the positions of the homothetic centersremain the same. This fact provides a (slotted) Linkage for converting circular motion with one radius to circularmotion with another.
The six homothetic centers of three circles lie three by three on four lines (Johnson 1929, p. 120), which ``enclose'' thesmallest circle.
The homothetic center of triangles is the Perspective Center of Homothetic Triangles. It is also called the Similitude Center (Johnson 1929, pp. 16-17).
See also Apollonius' Problem, Perspective, Similitude Center
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929.
Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.
- Zero
- Zero Divisor
- Zero (Root)
- Zero-Sum Game
- Zeta Fuchsian
- Zeta Function
- Zeuthen's Rule
- Zeuthen's Theorem
- Zig Number
- Zigzag Permutation
- Zig-Zag Triangle
- Zillion
- Zipf's Law
- Z-Number
- Zollner's Illusion
- Zonal Harmonic
- Zone
- Zonohedron
- Zonotype
- Zorn's Lemma
- z-Score
- Zsigmondy Theorem
- Z-Transform
- z-Transform
- z-Transform (Population)