Projective Plane
A projective plane is derived from a usual Plane by addition of a Line at Infinity. A projective plane oforder 
is a set of 
Points with the properties that:
- 1. Any two Points determine a Line,
- 2. Any two Lines determine a Point,
- 3. Every Point has
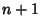Lines on it, and - 4. Every Line contains Points.
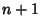, , 1) Block Design.An Affine Plane of order exists Iff a projective plane of order exists.A finite projective plane exists when the order is a Power of a Prime,i.e., 
for 
. It is conjectured that these are the only possible projective planes, but proving this remains one of the mostimportant unsolved problems in Combinatorics. The first few orders which are not of this form are 6, 10, 12, 14,15, ....
It has been proven analytically that there are no projective planes of order 6. By answering Lam'sProblem in the negative using massive computer calculations on top of some mathematics, it has been proved thatthere are no finite projective planes of order 10 (Lam 1991). The status of the order 12 projective plane remains open. The remarkable Bruck-Ryser-Chowla Theorem says that if a projective plane of order exists,and 
or 2 (mod 4), then is the sum of two Squares. This rules out 
.
The projective plane of order 2, also known as the Fano Plane, is denoted PG(2, 2).It has Incidence Matrix
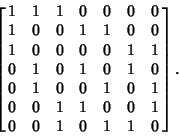
Every row and column contains 3 1s, and any pair of rows/columns has a single 1 in common.
The projective plane has Euler Characteristic 1, and the Heawood Conjecture therefore shows thatany set of regions on it can be colored using six colors only (Saaty 1986).
See also Affine Plane, Bruck-Ryser-Chowla Theorem, Fano Plane, Lam's Problem, Map Coloring, Moufang Plane,Projective Plane PK2, Real Projective Plane
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 281-287, 1987. Lam, C. W. H. ``The Search for a Finite Projective Plane of Order 10.'' Amer. Math. Monthly 98, 305-318, 1991. Lindner, C. C. and Rodger, C. A. Design Theory. Boca Raton, FL: CRC Press, 1997. Pinkall, U. ``Models of the Real Projective Plane.'' Ch. 6 in Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, pp. 63-67, 1986. Saaty, T. L. and Kainen, P. C. The Four-Color Problem: Assaults and Conquest. New York: Dover, p. 45, 1986.
- Conoid
- Consecutive Number Sequences
- Conservation of Number Principle
- Conservative Field
- Consistency
- Consistency Strength
- Constant
- Constant Function
- Constant Precession Curve
- Constant Problem
- Constant Width Curve
- Constructible Number
- Constructible Polygon
- Construction
- Constructive Dilemma
- Contact Angle
- Contact Number
- Contact Triangle
- Content
- Contiguous Function
- Continued Fraction
- Continued Fraction Constant
- Continued Fraction Factorization Algorithm
- Continued Fraction Fundamental Recurrence Relation
- Continued Fraction Map