Hyperbolic Geometry
A Non-Euclidean Geometry, also called Lobachevsky-Bolyai-Gauss Geometry, having constant Sectional Curvature 
. This Geometry satisfies all of Euclid'sPostulates except the Parallel Postulate, which is modified to read: For any infinite straight Line
and any Point 
not on it, there are many other infinitely extending straight Lines thatpass through and which do not intersect .
In hyperbolic geometry, the sum of Angles of a Triangle is less than 180°, andTriangles with the same angles have the same areas. Furthermore, not all Triangleshave the same Angle sum (c.f. the AAA Theorem for Triangles in Euclidean 2-space). Thebest-known example of a hyperbolic space are Spheres in Lorentzian 4-space. The PoincaréHyperbolic Disk is a hyperbolic 2-space. Hyperbolic geometry is well understood in 2-D, but notin 3-D.
Geometric models of hyperbolic geometry include the Klein-Beltrami Model, which consists of an Open Disk inthe Euclidean plane whose open chords correspond to hyperbolic lines. A 2-D model is the Poincaré HyperbolicDisk. Felix Klein 
constructed an analytic hyperbolic geometry in 1870in which a Point is represented by a pair of Real Numbers 
with
(i.e., points of an Open Disk in the Complex Plane) and the distance between two points is given by
The geometry generated by this formula satisfies all of Euclid's Postulates except the fifth.The Metric of this geometry is given by the Cayley-Klein-Hilbert Metric,
 |  |  | |
 | |  | |
 | |  |
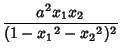Hilbert
extended the definition to general bounded sets in a Euclidean Space.See also Elliptic Geometry, Euclidean Geometry, Hyperbolic Metric, Klein-Beltrami Model,Non-Euclidean Geometry, Schwarz-Pick Lemma
References
Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 57-60, 1990. Eppstein, D. ``Hyperbolic Geometry.''http://www.ics.uci.edu/~eppstein/junkyard/hyper.html. Stillwell, J. Sources of Hyperbolic Geometry. Providence, RI: Amer. Math. Soc., 1996.
- Denjoy Integral
- Denominator
- Dense
- Density
- Density (Polygon)
- Density (Sequence)
- Denumerable Set
- Denumerably Infinite
- de Polignac's Conjecture
- Depth (Graph)
- Depth (Size)
- Depth (Statistics)
- Depth (Tree)
- Derangement
- de Rham Cohomology
- Derivative
- Derivative Test
- Derived Set
- Dervish
- Desargues' Theorem
- Descartes Circle Theorem
- Descartes-Euler Polyhedral Formula
- Descartes Folium
- Descartes' Formula
- Descartes Ovals