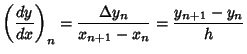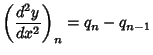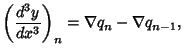| 释义 |
Adams' MethodAdams' method is a numerical Method for solving linear First-Order Ordinary Differential Equations of the form
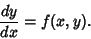 | (1) |
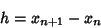 | (2) |
 about about  , ,
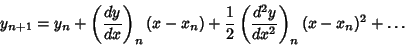 | (3) |
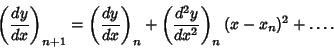 | (4) |
 are given by the Backward Differences are given by the Backward Differences
etc. Note that by (1), 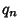 is just the value of is just the value of 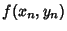 . .
For first-order interpolation, the method proceeds by iterating the expression
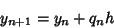 | (8) |
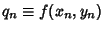 . The method can then be extended to arbitrary order using the finite differenceintegration formula from Beyer (1987) . The method can then be extended to arbitrary order using the finite differenceintegration formula from Beyer (1987)
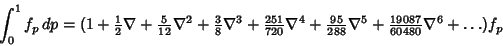 | (9) |
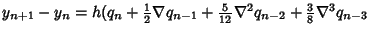 | | 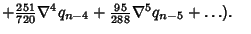 | (10) |
Note that von Kármán and Biot (1940) confusingly use the symbol normally used for Forward Differences 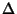 to denote Backward Differences to denote Backward Differences  .See also Gill's Method, Milne's Method, Predictor-Corrector Methods,Runge-Kutta Method .See also Gill's Method, Milne's Method, Predictor-Corrector Methods,Runge-Kutta Method
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 896, 1972.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 455, 1987. Kármán, T. von and Biot, M. A. Mathematical Methods in Engineering: An Introduction to the Mathematical Treatment of Engineering Problems. New York: McGraw-Hill, pp. 14-20, 1940. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, p. 741, 1992. |