Knight's Tour

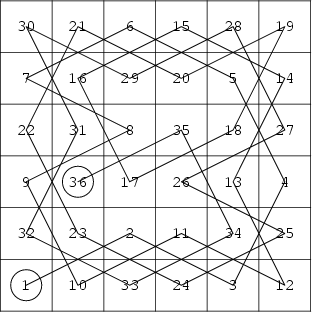
A knight's tour of a Chessboard (or any other grid) is a sequence of moves by a knight Chess piece (which mayonly make moves which simultaneously shift one square along one axis and two along the other) such that each square of theboard is visited exactly once (i.e., a Hamiltonian Circuit). If the final position is a knight's move away from the first position, the tour is called re-entrant. The first figure above shows a knight's tour on a Chessboard.The second set of figures shows six knight's tours on an Chessboard, all but the first of which arere-entrant. The final tour has the additional property that it is a Semimagic Square with row and column sums of 260 andmain diagonal sums of 348 and 168.

Löbbing and Wegener (1996) computed the number of cycles covering the directed knight's graph for an Chessboard. They obtained , where , i.e., 8,121,130,233,753,702,400. They alsocomputed the number of undirected tours, obtaining an incorrect answer 33,439,123,484,294 (which is not divisible by 4 asit must be), and so are currently redoing the calculation.

The following results are given by Kraitchik (1942). The number of possible tours on a board for , 4,... are 8, 0, 82, 744, 6378, 31088, 189688, 1213112, ... (Kraitchik 1942, p. 263). There are 14 tours on the rectangle, two of which are symmetrical. There are 376 tours on the rectangle, none of which is closed. Thereare 16 symmetric tours on the rectangle and 8 closed tours on the rectangle. There are 58 symmetrictours on the rectangle and 28 closed tours on the rectangle. There are five doubly symmetric tourson the square. There are 1728 tours on the square, 8 of which are symmetric. The longest``uncrossed'' knight's tours on an board for , 4, ... are 2, 5, 10, 17, 24, 35, ... (Sloane's A003192).

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 175-186, 1987.

Chartrand, G. ``The Knight's Tour.'' §6.2 in Introductory Graph Theory. New York: Dover, pp. 133-135, 1985.

Gardner, M. ``Knights of the Square Table.'' Ch. 14 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 188-202, 1978.

Guy, R. K. ``The Queens Problem.'' §C18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.

Kraitchik, M. ``The Problem of the Knights.'' Ch. 11 in Mathematical Recreations. New York: W. W. Norton, pp. 257-266, 1942.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 87-89, 1979.

Ruskey, F. ``Information on the Knight's Tour Problem.'' http://sue.csc.uvic.ca/~cos/inf/misc/Knight.html.

Sloane, N. J. A. SequencesA003192/M1369and A006075/M3224in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

van der Linde, A. Geschichte und Literatur des Schachspiels, Vol. 2. Berlin, pp. 101-111, 1874.

Volpicelli, P. ``Soluzione completa e generale, mediante la geometria di situazione, del problema relativo alle corse del cavallo sopra qualunque scacchiere.'' Atti della Reale Accad. dei Lincei 25, 87-162, 1872.

Wegener, I. and Löbbing, M. ``The Number of Knight's Tours Equals 33,439,123,484,294--Counting with Binary Decision Diagrams.'' Electronic J. Combinatorics 3, R5 1-4, 1996.http://www.combinatorics.org/Volume_3/volume3.html#R5.

• Shoemaker's Knife
• Shoe Surface
• Shortening
• Shuffle
• Siamese Dodecahedron
• Siamese Method
• Sibling
• Sicherman Dice
• Sici Spiral
• Side
• Sidon Sequence
• Siegel Disk Fractal
• Siegel Modular Function
• Siegel's Paradox
• Siegel's Theorem
• Sierpinski Arrowhead Curve
• Sierpinski Carpet
• Sierpinski Constant
• Sierpinski Curve
• Sierpinski Gasket
• Sierpinski-Menger Sponge
• Sierpinski Number of the First Kind
• Sierpinski Number of the Second Kind
• Sierpinski's Composite Number Theorem
• Sierpinski Sieve