| 释义 |
Kronecker DeltaThe simplest interpretation of the Kronecker delta is as the discrete version of the Delta Function defined by
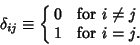 | (1) |
 | (2) |
 and and  are Integers. In 3-space, the Kronecker delta satisfies the identities are Integers. In 3-space, the Kronecker delta satisfies the identities
 | (3) |
 | (4) |
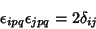 | (5) |
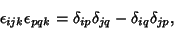 | (6) |
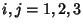 , and , and 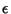 is the Permutation Symbol. is the Permutation Symbol.
Technically, the Kronecker delta is a Tensor defined by the relationship
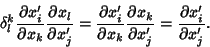 | (7) |
 and and  are independent for are independent for 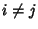 , ,
 | (8) |
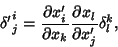 | (9) |
 is really a mixed second Rank Tensor. It satisfies is really a mixed second Rank Tensor. It satisfies
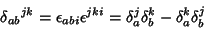 | (10) |
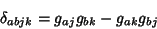 | (11) |
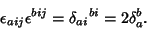 | (12) |
|