“Lagrange Interpolating Polynomial”的概念、定义、习题解题方法及翻译-数学辞典

单词

Lagrange Interpolating Polynomial

释义

Lagrange Interpolating Polynomial

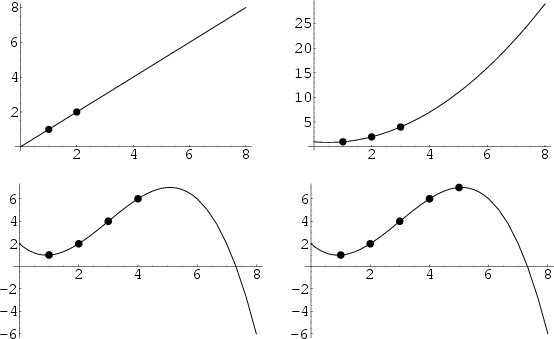
The Lagrange interpolating polynomial is the Polynomial of degree which passes through the points, , ..., . It is given by

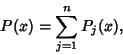(1)

where

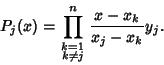(2)

Written explicitly,



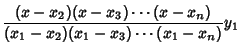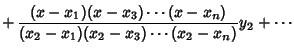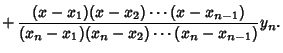			(3)

For

points,

			(4)
			(5)

Note that the function

passes through the points

, as can be seen for the case

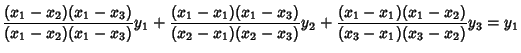			(6)
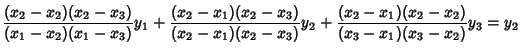			(7)
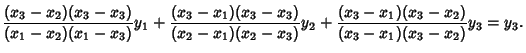			(8)

Generalizing to arbitrary

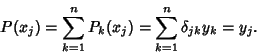(9)

The Lagrange interpolating polynomials can also be written using

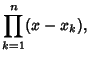			(10)
			(11)
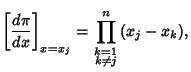			(12)

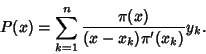(13)

Lagrange interpolating polynomials give no error estimate. A more conceptually straightforward method for calculatingthem is Neville's Algorithm.

See also Aitken Interpolation, Lebesgue Constants (Lagrange Interpolation), Neville's Algorithm,Newton's Divided Difference Interpolation Formula

References

Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 878-879 and 883, 1972.

Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 439, 1987.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Polynomial Interpolation and Extrapolation'' and ``Coefficients of the Interpolating Polynomial.'' §3.1 and 3.5 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 102-104 and 113-116, 1992.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。