| 释义 |
Landau-Kolmogorov ConstantsN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Let  be the Supremum of be the Supremum of  , a real-valued function , a real-valued function 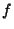 defined on defined on  . If . If 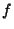 is twicedifferentiable and both is twicedifferentiable and both 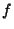 and and  are bounded, Landau (1913) showed that are bounded, Landau (1913) showed that
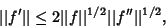 | (1) |
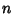 th derivative of th derivative of 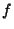 defined on defined on if both if both 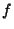 and and  are bounded, are bounded,
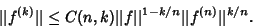 | (2) |
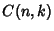 is not known, but particular cases are is not known, but particular cases are
Let  be the Supremum of be the Supremum of  , a real-valued function , a real-valued function 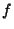 defined on defined on  . If . If 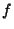 istwice differentiable and both istwice differentiable and both 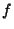 and and  are bounded, Hadamard (1914) showed that are bounded, Hadamard (1914) showed that
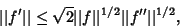 | (8) |
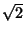 is the best possible. Kolmogorov (1962) determined the best constants is the best possible. Kolmogorov (1962) determined the best constants 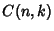 for for
 | (9) |
 | (10) |
 | (11) |
 |  |  | (12) | 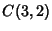 |  | 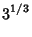 | (13) | 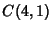 |  |  | (14) | 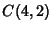 |  | 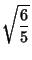 | (15) |  |  | 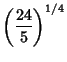 | (16) | 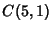 |  | 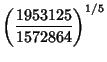 | (17) |  |  | 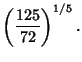 | (18) |
For a real-valued function 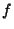 defined on defined on  , define , define
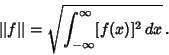 | (19) |
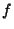 is is 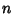 differentiable and both differentiable and both 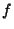 and and  are bounded, Hardy et al. (1934) showed that are bounded, Hardy et al. (1934) showed that
 | (20) |
 is the best possible for all is the best possible for all 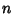 and and  . .
For a real-valued function 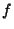 defined on defined on  , define , define
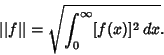 | (21) |
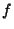 is twice differentiable and both is twice differentiable and both 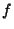 and and  are bounded, Hardy et al. (1934) showed that are bounded, Hardy et al. (1934) showed that
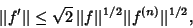 | (22) |
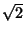 is the best possible. This inequality was extended by Ljubic (1964) and Kupcov (1975) to is the best possible. This inequality was extended by Ljubic (1964) and Kupcov (1975) to
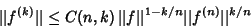 | (23) |
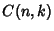 are given in terms of zeros of Polynomials. Special cases are are given in terms of zeros of Polynomials. Special cases are
 |  | 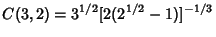 | | | |  |  | (24) | 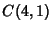 |  | 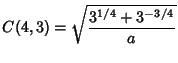 | | | |  | 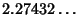 | (25) | 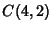 |  | 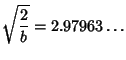 | (26) |  |  | 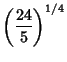 | (27) | 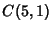 |  | 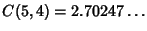 | (28) |  |  |  | (29) |
where 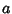 is the least Positive Root of is the least Positive Root of
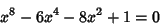 | (30) |
 is the least Positive Root of is the least Positive Root of
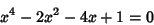 | (31) |
 are given by are given by
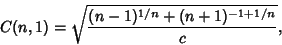 | (32) |
 is the least Positive Root of is the least Positive Root of
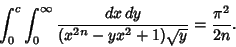 | (33) |
 . .
The cases 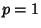 , 2, , 2,  are the only ones for which the best constants have exact expressions (Kwong and Zettl 1992,Franco et al. 1983). are the only ones for which the best constants have exact expressions (Kwong and Zettl 1992,Franco et al. 1983).
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lk/lk.htmlFranco, Z. M.; Kaper, H. G.; Kwong, M. N.; and Zettl, A. ``Bounds for the Best Constants in Landau's Inequality on the Line.'' Proc. Roy. Soc. Edinburgh 95A, 257-262, 1983. Franco, Z. M.; Kaper, H. G.; Kwong, M. N.; and Zettl, A. ``Best Constants in Norm Inequalities for Derivatives on a Half Line.'' Proc. Roy. Soc. Edinburgh 100A, 67-84, 1985. Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities. Cambridge, England: Cambridge University Press, 1934. Kolmogorov, A. ``On Inequalities Between the Upper Bounds of the Successive Derivatives of an Arbitrary Function on an Infinite Integral.'' Amer. Math. Soc. Translations, Ser. 1 2, 233-243, 1962. Kupcov, N. P. ``Kolmogorov Estimates for Derivatives in  .'' Proc. Steklov Inst. Math. 138, 101-125, 1975. .'' Proc. Steklov Inst. Math. 138, 101-125, 1975. Kwong, M. K. and Zettl, A. Norm Inequalities for Derivatives and Differences. New York: Springer-Verlag, 1992. Landau, E. ``Einige Ungleichungen für zweimal differentzierbare Funktionen.'' Proc. London Math. Soc. Ser. 2 13, 43-49, 1913. Landau, E. ``Die Ungleichungen für zweimal differentzierbare Funktionen.'' Danske Vid. Selsk. Math. Fys. Medd. 6, 1-49, 1925. Ljubic, J. I. ``On Inequalities Between the Powers of a Linear Operator.'' Amer. Math. Soc. Trans. Ser. 2 40, 39-84, 1964. Neta, B. ``On Determinations of Best Possible Constants in Integral Inequalities Involving Derivatives.'' Math. Comput. 35, 1191-1193, 1980. Schoenberg, I. J. ``The Elementary Case of Landau's Problem of Inequalities Between Derivatives.'' Amer. Math. Monthly 80, 121-158, 1973.
|
![]() be the Supremum of
be the Supremum of ![]() , a real-valued function
, a real-valued function ![]() defined on
defined on ![]() . If
. If ![]() is twicedifferentiable and both
is twicedifferentiable and both ![]() and
and ![]() are bounded, Landau (1913) showed that
are bounded, Landau (1913) showed that
![]() be the Supremum of
be the Supremum of ![]() , a real-valued function
, a real-valued function ![]() defined on
defined on ![]() . If
. If ![]() istwice differentiable and both
istwice differentiable and both ![]() and
and ![]() are bounded, Hadamard (1914) showed that
are bounded, Hadamard (1914) showed that


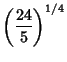
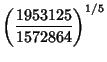
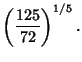
![]() defined on
defined on ![]() , define
, define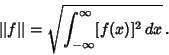
![]() defined on
defined on ![]() , define
, define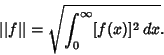
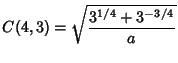
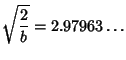
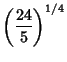
![]() , 2,
, 2, ![]() are the only ones for which the best constants have exact expressions (Kwong and Zettl 1992,Franco et al. 1983).
are the only ones for which the best constants have exact expressions (Kwong and Zettl 1992,Franco et al. 1983).![]() .'' Proc. Steklov Inst. Math. 138, 101-125, 1975.
.'' Proc. Steklov Inst. Math. 138, 101-125, 1975.