| 释义 |
Lane-Emden Differential EquationA second-order Ordinary Differential Equation arising in the study of stellar interiors. It is given by
 | (1) |
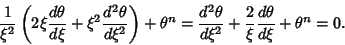 | (2) |
Solutions 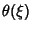 for for 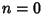 , 1, 2, 3, and 4 are shown above. The cases , 1, 2, 3, and 4 are shown above. The cases 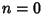 , 1, and 5 can be solved analytically(Chandrasekhar 1967, p. 91); the others must be obtained numerically. , 1, and 5 can be solved analytically(Chandrasekhar 1967, p. 91); the others must be obtained numerically.
For 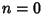 ( (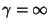 ), the Lane-Emden Differential Equation is ), the Lane-Emden Differential Equation is
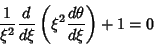 | (5) |
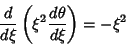 | (6) |
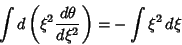 | (7) |
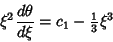 | (8) |
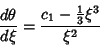 | (9) |
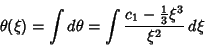 | (10) |
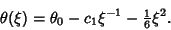 | (11) |
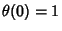 then gives then gives 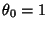 and and 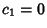 , so , so
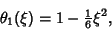 | (12) |
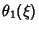 is Parabolic. is Parabolic.
For 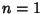 ( ( ), the differential equation becomes ), the differential equation becomes
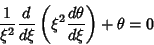 | (13) |
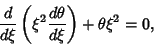 | (14) |
 | (15) |
 and and 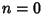 , so the solution is , so the solution is
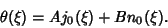 | (16) |
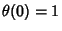 gives gives
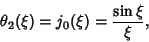 | (17) |
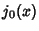 is a Spherical Bessel Function of the First Kind (Chandrasekhar 1967, pp. 92). is a Spherical Bessel Function of the First Kind (Chandrasekhar 1967, pp. 92).
For 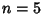 , make Emden's transformation , make Emden's transformation
which reduces the Lane-Emden equation to
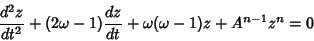 | (20) |
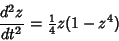 | (21) |
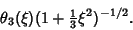 | (22) |
References
Chandrasekhar, S. An Introduction to the Study of Stellar Structure. New York: Dover, pp. 84-182, 1967.
|


![]() (
(![]() ), the Lane-Emden Differential Equation is
), the Lane-Emden Differential Equation is![]() (
(![]() ), the differential equation becomes
), the differential equation becomes ![]() , make Emden's transformation
, make Emden's transformation