Linearly Dependent Vectors
Vectors 
, 
, ..., 
are linearly dependent Iff thereexist Scalars 
, 
, ..., 
, not all zero, such that
 | (1) |
, ..., . If no such Scalars exist,then the vectors are said to be linearly independent. In order to satisfy the Criterion for linear dependence, | (2) |
 | (3) |
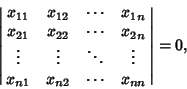 | (4) |
Let 
and 
be -D Vectors. Then the following three conditions are equivalent(Gray 1993).
- 1. and are linearly dependent.
- 2.
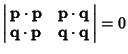. - 3. The
Matrix 
has rank less than two.
References
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 186-187, 1993.
- Connected Sum
- Connected Sum Decomposition
- Connection
- Connection Coefficient
- Connectivity
- Connes Function
- Conocuneus of Wallis
- Conoid
- Consecutive Number Sequences
- Conservation of Number Principle
- Conservative Field
- Consistency
- Consistency Strength
- Constant
- Constant Function
- Constant Precession Curve
- Constant Problem
- Constant Width Curve
- Constructible Number
- Constructible Polygon
- Construction
- Constructive Dilemma
- Contact Angle
- Contact Number
- Contact Triangle