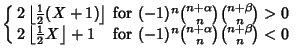| 释义 |
Jacobi PolynomialAlso known as the Hypergeometric Polynomials, they occur in the study ofRotation Groups and in the solution to the equations of motion of the symmetrictop.  They are solutions to the Jacobi Differential Equation. Plugging They are solutions to the Jacobi Differential Equation. Plugging
 | (1) |
 | (2) |
 , 1, ..., where , 1, ..., where
 | (3) |
 | (4) |
 . They form a complete orthogonal system in the interval . They form a complete orthogonal system in the interval 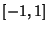 with respect to the weightingfunction with respect to the weightingfunction
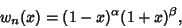 | (5) |
 | (6) |
 is a Binomial Coefficient. Jacobi polynomials can also be written is a Binomial Coefficient. Jacobi polynomials can also be written
 | (7) |
 is the Gamma Function and is the Gamma Function and
 | (8) |
Jacobi polynomials are Orthogonal satisfying
 | (9) |
 in in  is given by is given by
 | (10) |
 is the Rising Factorial is the Rising Factorial
 | (12) |
The Derivative is given by
 | (13) |
The Orthogonal Polynomials with Weighting Function  on the Closed Interval on the Closed Interval  can be expressed in the form can be expressed in the form
 | (14) |
Special cases with  are are
Further identities are
 | (19) |
 | (20) |
 | | 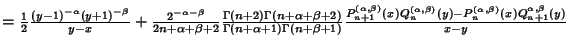 | (21) |
(Szegö 1975, p. 79).
The Kernel Polynomial is  | | 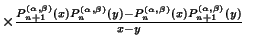 | (22) |
(Szegö 1975, p. 71).
The Discriminant is
 | (23) |
For  , , 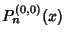 reduces to a Legendre Polynomial. The Gegenbauer Polynomial reduces to a Legendre Polynomial. The Gegenbauer Polynomial
 | (24) |
 | (25) |
 | (26) |
Let  be the number of zeros in be the number of zeros in  , ,  the number of zeros in the number of zeros in  , and , and  thenumber of zeros in thenumber of zeros in  . Define Klein's symbol . Define Klein's symbol
 | (27) |
 is the Floor Function, and is the Floor Function, and
If the cases  , ,  , ..., , ..., 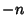 , ,  , ,  , ..., , ..., 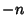 , and , and  , ,  , ..., , ..., 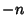 are excluded, then the number of zeros of are excluded, then the number of zeros of  in the respective intervals are in the respective intervals are
(Szegö 1975, pp. 144-146).
The first few Polynomials are
where  is a Rising Factorial. See Abramowitz and Stegun (1972, pp. 782-793) and Szegö (1975, Ch. 4) foradditional identities.See also Chebyshev Polynomial of the First Kind, Gegenbauer Polynomial, Jacobi Function of the SecondKind, Rising Factorial, Zernike Polynomial is a Rising Factorial. See Abramowitz and Stegun (1972, pp. 782-793) and Szegö (1975, Ch. 4) foradditional identities.See also Chebyshev Polynomial of the First Kind, Gegenbauer Polynomial, Jacobi Function of the SecondKind, Rising Factorial, Zernike Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.Iyanaga, S. and Kawada, Y. (Eds.). ``Jacobi Polynomials.'' Appendix A, Table 20.V in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1480, 1980. Szegö, G. ``Jacobi Polynomials.'' Ch. 4 in Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975. |
![]() They are solutions to the Jacobi Differential Equation. Plugging
They are solutions to the Jacobi Differential Equation. Plugging
![]() on the Closed Interval
on the Closed Interval ![]() can be expressed in the form
can be expressed in the form![]() are
are



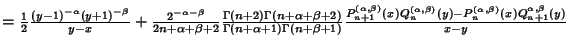
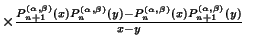

![]() ,
, ![]() reduces to a Legendre Polynomial. The Gegenbauer Polynomial
reduces to a Legendre Polynomial. The Gegenbauer Polynomial![]() be the number of zeros in
be the number of zeros in ![]() ,
, ![]() the number of zeros in
the number of zeros in ![]() , and
, and ![]() thenumber of zeros in
thenumber of zeros in ![]() . Define Klein's symbol
. Define Klein's symbol