| 释义 |
Logistic EquationThe logistic equation (sometimes called the Verhulst Model since it was first published in 1845 by the BelgianP.-F. Verhulst) is defined by
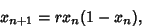 | (1) |
 (sometimes also denoted (sometimes also denoted 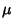 ) is a Positive constant (the ``biotic potential''). We will start ) is a Positive constant (the ``biotic potential''). We will start 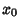 in theinterval in theinterval 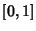 . In order to keep points in the interval, we must find appropriate conditions on . In order to keep points in the interval, we must find appropriate conditions on  . The maximumvalue . The maximumvalue  can take is found from can take is found from
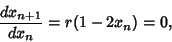 | (2) |
 occurs for occurs for 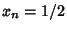 . Plugging this in, . Plugging this in,  . Therefore, tokeep the Map in the desired region, we must have . Therefore, tokeep the Map in the desired region, we must have  . The Jacobian is . The Jacobian is
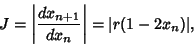 | (3) |
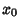 if if 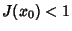 . Now we wish to find the Fixed Points of the Map, which occur when . Now we wish to find the Fixed Points of the Map, which occur when 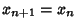 . Drop the . Drop the  subscript on subscript on 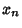
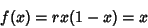 | (4) |
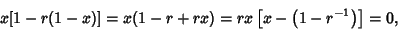 | (5) |
 and and 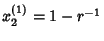 . An interesting thing happens ifa value of . An interesting thing happens ifa value of  greater than 3 is chosen. The map becomes unstable and we get a Pitchfork Bifurcation with twostable orbits of period two corresponding to the two stable Fixed Points of greater than 3 is chosen. The map becomes unstable and we get a Pitchfork Bifurcation with twostable orbits of period two corresponding to the two stable Fixed Points of  . The fixedpoints of order two must satisfy . The fixedpoints of order two must satisfy 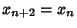 , so , so
Now, drop the 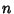 subscripts and rewrite subscripts and rewrite
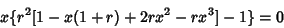 | (7) |
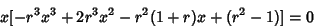 | (8) |
 | (9) |
These solutions are only Real for 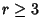 , so this is where the 2-Cycle begins. Now look for the onset of the 4-Cycle. To eliminate the 2- and 1-Cycles, consider , so this is where the 2-Cycle begins. Now look for the onset of the 4-Cycle. To eliminate the 2- and 1-Cycles, consider
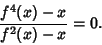 | (11) |
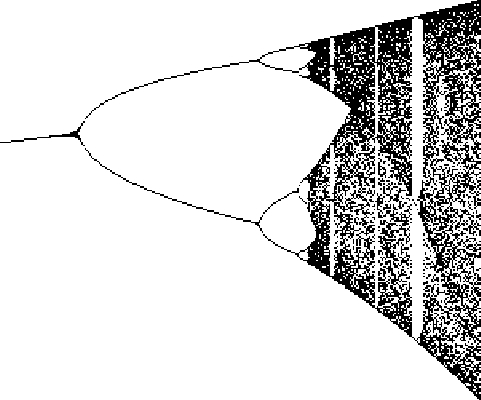
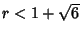 , but two of themconvert to Real roots at this value (although this is difficult to show except by plugging in). The4-Cycle therefore starts at , but two of themconvert to Real roots at this value (although this is difficult to show except by plugging in). The4-Cycle therefore starts at  . The Bifurcations comefaster and faster (8, 16, 32, ...), then suddenly break off. Beyond a certain point known as the Accumulation Point,periodicity gives way to Chaos. . The Bifurcations comefaster and faster (8, 16, 32, ...), then suddenly break off. Beyond a certain point known as the Accumulation Point,periodicity gives way to Chaos.A table of the Cycle type and value of 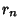 at which the cycle at which the cycle 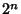 appears is given below. appears is given below.
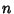 | cycle (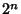 ) ) | 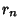 | | 1 | 2 | 3 | | 2 | 4 | 3.449490 | | 3 | 8 | 3.544090 | | 4 | 16 | 3.564407 | | 5 | 32 | 3.568750 | | 6 | 64 | 3.56969 | | 7 | 128 | 3.56989 | | 8 | 256 | 3.569934 | | 9 | 512 | 3.569943 | | 10 | 1024 | 3.5699451 | | 11 | 2048 | 3.569945557 |  | acc. pt. | 3.569945672 |
For additional values, see Rasband (1990, p. 23). Note that the table in Tabor (1989, p. 222) is incorrect, as is the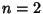 entry in Lauwerier (1991). In the middle of the complexity, a window suddenly appears with a regular period like 3or 7 as a result of Mode Locking. The period 3 Bifurcation occurs at entry in Lauwerier (1991). In the middle of the complexity, a window suddenly appears with a regular period like 3or 7 as a result of Mode Locking. The period 3 Bifurcation occurs at  , as isderived below. Following the 3-Cycle, the Period Doublings then beginagain with Cycles of 6, 12, ...and 7, 14, 28, ..., and then once again break off toChaos. , as isderived below. Following the 3-Cycle, the Period Doublings then beginagain with Cycles of 6, 12, ...and 7, 14, 28, ..., and then once again break off toChaos.
A set of 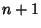 equations which can be solved to give the onset of an arbitrary equations which can be solved to give the onset of an arbitrary 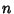 -cycle (Saha and Strogatz1995) is -cycle (Saha and Strogatz1995) is
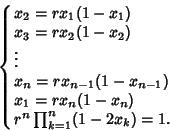 | (13) |
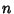 of these give of these give 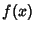 , ,  , ..., , ..., 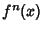 , and the last uses the fact that the onset of period , and the last uses the fact that the onset of period 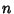 occurs by a Tangent Bifurcation, so the occurs by a Tangent Bifurcation, so the 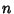 th Derivative is 1. th Derivative is 1.
For 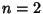 , the solutions ( , the solutions (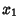 , ..., , ..., 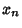 , ,  ) are (0, 0, ) are (0, 0, 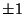 ) and ( ) and (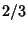 , , 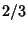 , 3), so the desiredBifurcation occurs at , 3), so the desiredBifurcation occurs at 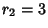 . Taking . Taking  gives gives
Solving the resulting Cubic Equation using computer algebra gives
where
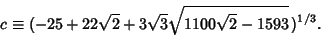 | (19) |
Saha and Strogatz (1995) give a simplified algebraic treatment which involves solving
 | (24) |
Further simplifications still are provided in Bechhoeffer (1996) and Gordon (1996), but neither of these techniques generalizeseasily to higher Cycles. Bechhoeffer (1996) expresses the three additional equations as
giving
 | (31) |
 -values supporting stable period 3 orbits. This value is obtained by solving the Cubic Equation -values supporting stable period 3 orbits. This value is obtained by solving the Cubic Equation
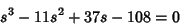 | (32) |
 , then , then
The logistic equation has Correlation Exponent  (Grassberger and Procaccia 1983), CapacityDimension 0.538 (Grassberger 1981), and Information Dimension 0.5170976 (Grassberger and Procaccia 1983). (Grassberger and Procaccia 1983), CapacityDimension 0.538 (Grassberger 1981), and Information Dimension 0.5170976 (Grassberger and Procaccia 1983). See also Bifurcation, Feigenbaum Constant, Logistic Distribution, LogisticEquation r=4, Logistic Growth Curve, Period Three Theorem, Quadratic Map
References
Bechhoeffer, J. ``The Birth of Period 3, Revisited.'' Math. Mag. 69, 115-118, 1996.Bogomolny, A. ``Chaos Creation (There is Order in Chaos).'' http://www.cut-the-knot.com/blue/chaos.html. Dickau, R. M. ``Bifurcation Diagram.''http://forum.swarthmore.edu/advanced/robertd/bifurcation.html. Gleick, J. Chaos: Making a New Science. New York: Penguin Books, pp. 69-80, 1988. Gordon, W. B. ``Period Three Trajectories of the Logistic Map.'' Math. Mag. 69, 118-120, 1996. Grassberger, P. ``On the Hausdorff Dimension of Fractal Attractors.'' J. Stat. Phys. 26, 173-179, 1981. Grassberger, P. and Procaccia, I. ``Measuring the Strangeness of Strange Attractors.'' Physica D 9, 189-208, 1983. Lauwerier, H. Fractals: Endlessly Repeated Geometrical Figures. Princeton, NJ: Princeton University Press, pp. 119-122, 1991. May, R. M. ``Simple Mathematical Models with Very Complicated Dynamics.'' Nature 261, 459-467, 1976. Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, pp. 585-653, 1992. Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, p. 23, 1990. Russell, D. A.; Hanson, J. D.; and Ott, E. ``Dimension of Strange Attractors.'' Phys. Rev. Let. 45, 1175-1178, 1980. Saha, P. and Strogatz, S. H. ``The Birth of Period Three.'' Math. Mag. 68, 42-47, 1995. Strogatz, S. H. Nonlinear Dynamics and Chaos. Reading, MA: Addison-Wesley, 1994. Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989. Wagon, S. ``The Dynamics of the Quadratic Map.'' §4.4 in Mathematica in Action. New York: W. H. Freeman, pp. 117-140, 1991. |
![]() at which the cycle
at which the cycle ![]() appears is given below.
appears is given below.![]() entry in Lauwerier (1991). In the middle of the complexity, a window suddenly appears with a regular period like 3or 7 as a result of Mode Locking. The period 3 Bifurcation occurs at
entry in Lauwerier (1991). In the middle of the complexity, a window suddenly appears with a regular period like 3or 7 as a result of Mode Locking. The period 3 Bifurcation occurs at ![]() , as isderived below. Following the 3-Cycle, the Period Doublings then beginagain with Cycles of 6, 12, ...and 7, 14, 28, ..., and then once again break off toChaos.
, as isderived below. Following the 3-Cycle, the Period Doublings then beginagain with Cycles of 6, 12, ...and 7, 14, 28, ..., and then once again break off toChaos.![]() equations which can be solved to give the onset of an arbitrary
equations which can be solved to give the onset of an arbitrary ![]() -cycle (Saha and Strogatz1995) is
-cycle (Saha and Strogatz1995) is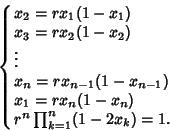
![]() , the solutions (
, the solutions (![]() , ...,
, ..., ![]() ,
, ![]() ) are (0, 0,
) are (0, 0, ![]() ) and (
) and (![]() ,
, ![]() , 3), so the desiredBifurcation occurs at
, 3), so the desiredBifurcation occurs at ![]() . Taking
. Taking ![]() gives
gives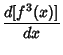
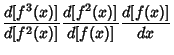
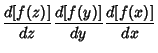
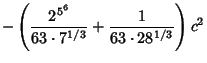
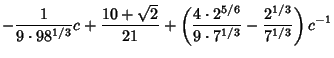
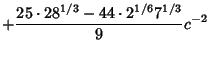
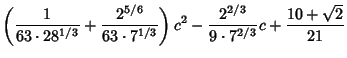
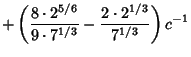
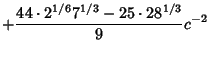

![]() (Grassberger and Procaccia 1983), CapacityDimension 0.538 (Grassberger 1981), and Information Dimension 0.5170976 (Grassberger and Procaccia 1983).
(Grassberger and Procaccia 1983), CapacityDimension 0.538 (Grassberger 1981), and Information Dimension 0.5170976 (Grassberger and Procaccia 1983).