| 释义 |
Maclaurin SeriesA series expansion of a function about 0,
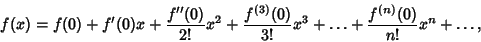 | (1) |
 Maclaurin series for common functions include Maclaurin series for common functions include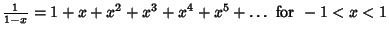 | (2) | 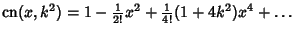 | (3) |  | (4) | 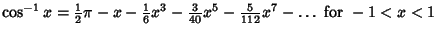 | (5) |  | (6) | 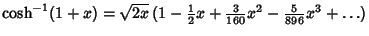 | (7) | 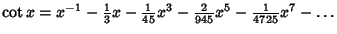 | (8) | 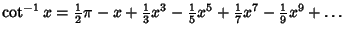 | (9) | 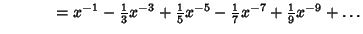 | (10) | 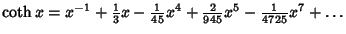 | (11) | 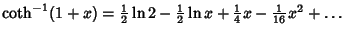 | (12) | 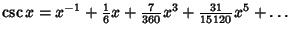 | (13) | 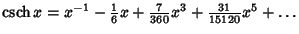 | (14) | 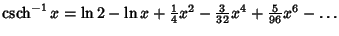 | (15) | 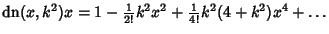 | (16) | 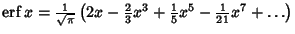 | (17) | 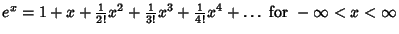 | (18) |
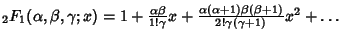 | (19) |  | (20) | 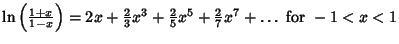 | (21) | 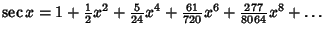 | (22) |  | (23) | 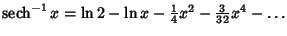 | (24) | 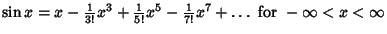 | (25) | 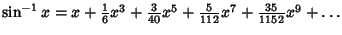 | (26) | 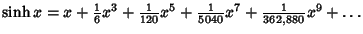 | (27) | 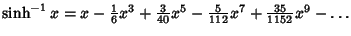 | (28) |  | (29) | 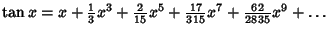 | (30) |  | (31) | 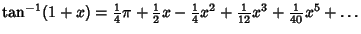 | (32) | 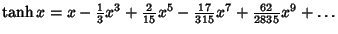 | (33) | 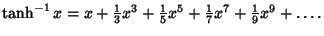 | (34) |
The explicit forms for some of these are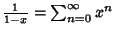 | (35) |  | (36) |  | (37) | 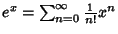 | (38) | 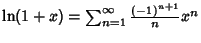 | (39) | 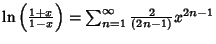 | (40) |  | (41) | 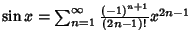 | (42) | 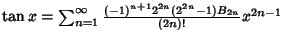 | (43) |  | (44) |  | (45) |
where 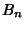 are Bernoulli Numbers and are Bernoulli Numbers and  are Euler Numbers.See also Alcuin's Sequence, Lagrange Expansion, Legendre Series, Taylor Series are Euler Numbers.See also Alcuin's Sequence, Lagrange Expansion, Legendre Series, Taylor Series
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 299-300, 1987.
|