| 释义 |
Matrix EquationNonhomogeneous matrix equations of the form
 | (1) |
 | (2) |
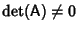 . In general,more numerically stable techniques of solving the equation include Gaussian Elimination, LU Decomposition, or theSquare Root Method. . In general,more numerically stable techniques of solving the equation include Gaussian Elimination, LU Decomposition, or theSquare Root Method.
For a homogeneous  Matrix equation Matrix equation
 | (3) |
 s, consider the Determinant s, consider the Determinant
 | (4) |
 , which is equivalent to multiplying the first column (or any column) by , which is equivalent to multiplying the first column (or any column) by  , ,
 | (5) |
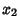 timescolumn 2, ..., and timescolumn 2, ..., and 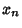 times column times column 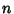 to the first column to obtain to the first column to obtain
 | (6) |
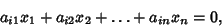 | (7) |
 | (8) |
 which is a solution, the Determinant is zero. This is also true for which is a solution, the Determinant is zero. This is also true for 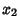 ,..., ,..., 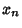 , so the original homogeneous system has a nontrivial solution for all , so the original homogeneous system has a nontrivial solution for all  s only if the Determinant is 0. This approach is the basis for Cramer's Rule. s only if the Determinant is 0. This approach is the basis for Cramer's Rule.
Given a numerical solution to a matrix equation, the solution can be iteratively improved using the followingtechnique. Assume that the numerically obtained solution to
 | (9) |
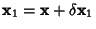 , where , where 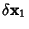 is an error term. The first solution therefore gives is an error term. The first solution therefore gives
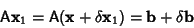 | (10) |
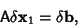 | (11) |
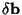 is found by solving (10) is found by solving (10)
 | (12) |
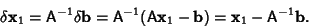 | (13) |
|
![]() Matrix equation
Matrix equation



