Motzkin Number

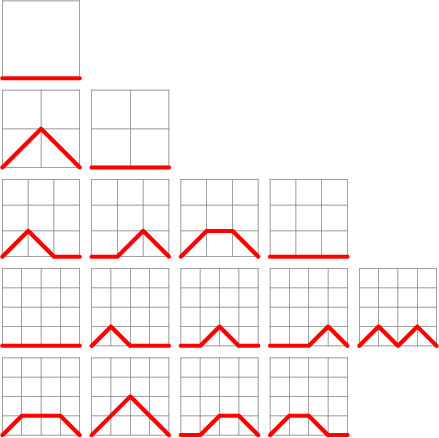
The Motzkin numbers enumerate various combinatorial objects. Donaghey and Shapiro (1977) give 14 different manifestations ofthese numbers. In particular, they give the number of paths from (0, 0) to (, 0) which never dip below and are madeup only of the steps (1, 0), (1, 1), and (1, ), i.e., , , and . The first are 1, 2, 4,9, 21, 51, ... (Sloane's A001006). The Motzkin number Generating Function satisfies

(1)

(2)

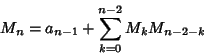(3)

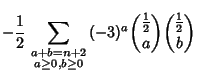			(4)
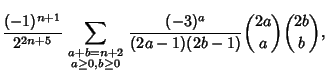			(5)

References

Barcucci, E.; Pinzani, R.; and Sprugnoli, R. ``The Motzkin Family.'' Pure Math. Appl. Ser. A 2, 249-279, 1991.

Donaghey, R. ``Restricted Plane Tree Representations of Four Motzkin-Catalan Equations.'' J. Combin. Th. Ser. B 22, 114-121, 1977.

Donaghey, R. and Shapiro, L. W. ``Motzkin Numbers.'' J. Combin. Th. Ser. A 23, 291-301, 1977.

Kuznetsov, A.; Pak, I.; and Postnikov, A. ``Trees Associated with the Motzkin Numbers.'' J. Combin. Th. Ser. A 76, 145-147, 1996.

Motzkin, T. ``Relations Between Hypersurface Cross Ratios, and a Combinatorial Formula for Partitions of a Polygon, for Permanent Preponderance, and for Nonassociative Products.'' Bull. Amer. Math. Soc. 54, 352-360, 1948.

Sloane, N. J. A. SequenceA001006/M1184in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

• Prime Polynomial
• Prime Power Conjecture
• Prime Power Symbol
• Primequad
• Prime Quadratic Effect
• Prime Quadruplet
• Prime Representation
• Prime Ring
• Prime Sequence
• Prime Spiral
• Prime String
• Prime Sum
• Prime Theta Function
• Prime Triangle
• Prime Unit
• Prime Zeta Function
• Primitive Abundant Number
• Primitive Function
• Primitive Irreducible Polynomial
• Primitive Polynomial Modulo 2
• Primitive Prime Factor
• Primitive Pseudoperfect Number
• Primitive Recursive Function
• Primitive Root
• Primitive Root of Unity