| 释义 |
Point-Point Distance--2-DGiven two points in the Plane, find the curve which minimizes the distance between them. The Line Element is given by
 | (1) |
 and and 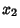 is is
 | (2) |
 and the quantity we are minimizing is and the quantity we are minimizing is
 | (3) |
so the Euler-Lagrange Differential Equation becomes
 | (6) |
 | (7) |
 | (8) |
 | (9) |
 | (10) |
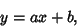 | (11) |
 and and 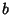 are determined from are determined from
Writing (12) and (13) as a Matrix Equation gives
 | (14) |
so
as expected.
The shortest distance between two points on a Sphere is the so-called Great Circle distance. See also Calculus of Variations, Great Circle, Point-Point Distance--1-D, Point-Point Distance--3-D,Point-Quadratic Distance, Tetrahedron Inscribing, Triangle Inscribing in a Circle
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 930-931, 1985. |