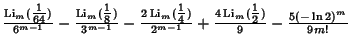| 释义 |
PolylogarithmThe function
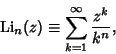 | (1) |
 is also used forthe Feynman Diagram is also used forthe Feynman Diagram  integrals, and the special case integrals, and the special case  is called the Dilogarithm. The polylogarithm of Negative Integer order arises in sums of the form is called the Dilogarithm. The polylogarithm of Negative Integer order arises in sums of the form
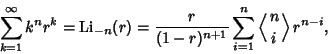 | (2) |
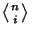 is an Eulerian Number. is an Eulerian Number.
The polylogarithm satisfies the fundamental identities
 | (3) |
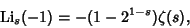 | (4) |
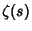 is the Riemann Zeta Function. The derivative is therefore given by is the Riemann Zeta Function. The derivative is therefore given by
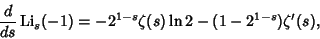 | (5) |
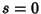 , by , by
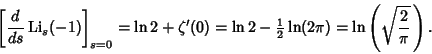 | (6) |
The polylogarithm identities lead to remarkable expressions. Ramanujan  gave the polylogarithm identities gave the polylogarithm identities
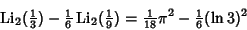 | (7) |
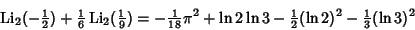 | (8) |
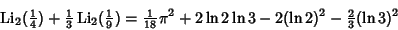 | (9) |
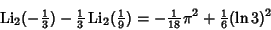 | (10) |
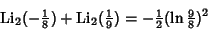 | (11) |
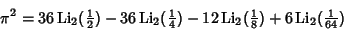 | (12) |
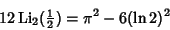 | (13) |
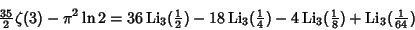 | (14) |
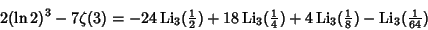 | (15) |
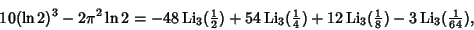 | (16) |
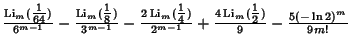 | |  | (17) |
No general Algorithm is know for the integration of polylogarithms of functions. See also Dilogarithm, Eulerian Number, Legendre's Chi-Function, Logarithmic Integral,Nielsen-Ramanujan Constants
References
Bailey, D.; Borwein, P.; and Plouffe, S. ``On the Rapid Computation of Various Polylogarithmic Constants.'' http://www.cecm.sfu.ca/~pborwein/PAPERS/P123.ps.Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 323-326, 1994. Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981. Lewin, L. (Ed.). Structural Properties of Polylogarithms. Providence, RI: Amer. Math. Soc., 1991. Nielsen, N. Der Euler'sche Dilogarithms. Leipzig, Germany: Halle, 1909. |
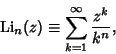
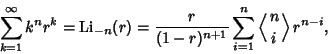
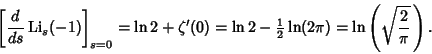
![]() gave the polylogarithm identities
gave the polylogarithm identities