√(a1– b1)2+ (a2– b2)2

√b12+ b22

√a12+ a22

How Many? Cost

2 Ham @$2.80 ———

Turkey @$3.15 ———

1 Egg Salad @$1.95 ———

3 Tuna @$2.50 ———

Roast Beef @$3.60 ———

Total Cost: ———

dot product 147

Triangle of vectors

divisor of zero Two quantities, neither of which are

zero, yet multiply together to give zero as their product

are called divisors of zero. In ordinary arithmetic, divi-

sors of zero never arise: if a×b= 0, then at least one of

aor bmust be zero. In

MODULAR ARITHMETIC

, however,

divisors of zero can exist. For example, 3 ×2 equals zero

in arithmetic modulo 6. Two nonzero matrices may mul-

tiply to give the zero

MATRIX

, and the product of two

nonzero functions could be the zero function.

The presence of zero divisors in a mathematical

system often complicates the arithmetic one can per-

form within that system. For example, for arithmetic

modulo 10, 2 ×4 equals 2 ×9, but dividing by 2, a

divisor of zero in this system, leads to the erroneous

conclusion that 4 and 9 are equal in this system. In

general, one can never perform division when a divisor

of zero is involved.

dot product (inner product, scalar product) Denoted

a·b, the dot product of two

VECTOR

s aand bis the sum

of the products of respective components of the vectors.

Precisely, if a= <a1,a2,…,an> and b= <b1,b2,…,bn>,

then a·bis the number:

a·b= a1b1+ a2b2+…+ anbn

The result of the dot product operation is always a real

number (scalar). For example, the dot product of the

two vectors a= < 1,4> and b= < 2,3> is a·b= 1 · 2 +

4 · 3 = 14.

The dot product arises in many situations. For

example, a local delicatessen receives the following

lunch order form:

One could interpret the order as a five-dimensional vec-

tor <2,0,1,3,0> to be matched with a five-dimensional

“cost vector” <2.80,3.15,1.95,2.50,3.60>. The total

cost of the order is then the dot product of these two

vectors:

2 ×2.80 + 0 ×3.15 + 1 ×1.95 + 3 ×2.50 + 0 ×3.60 =

$15.05

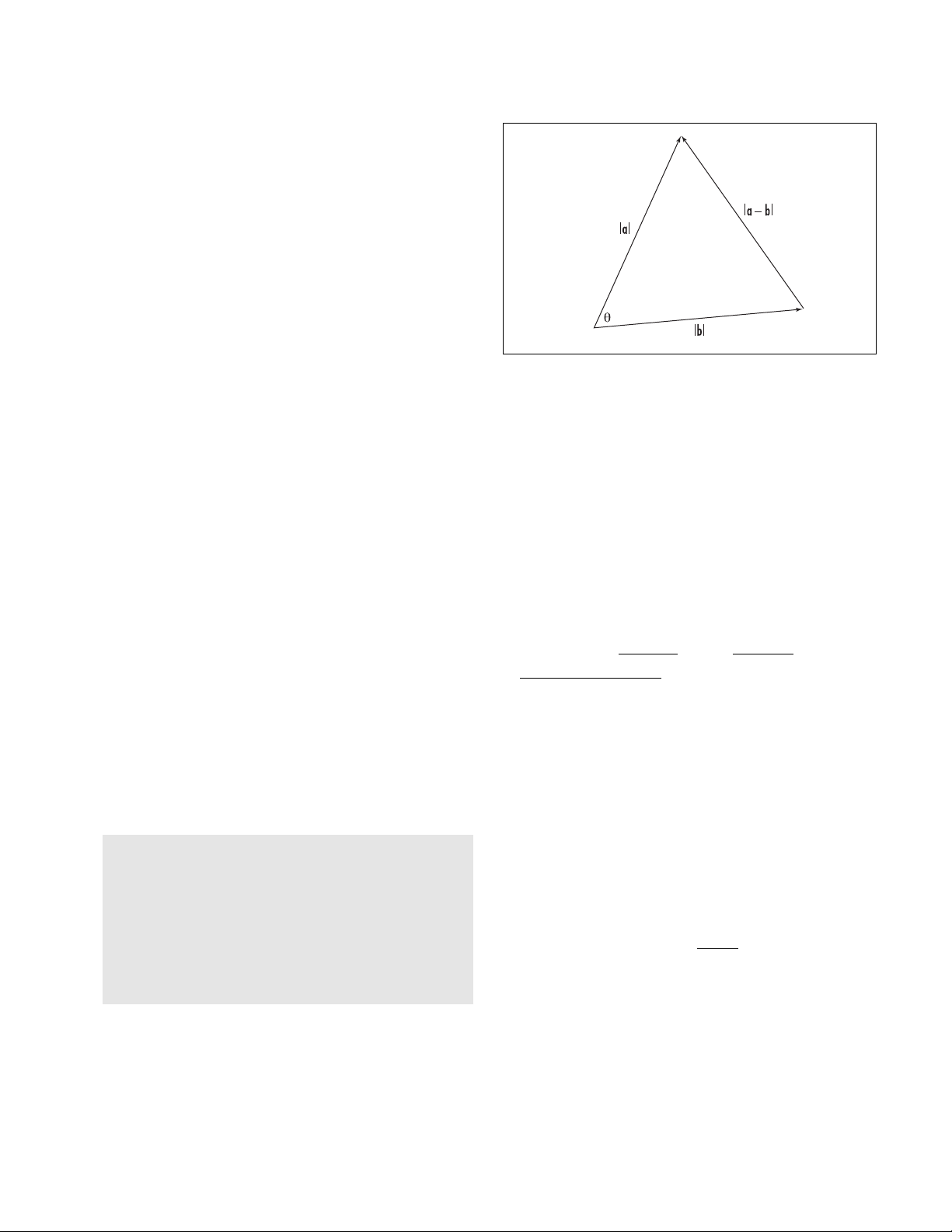
Geometrically, the dot product gives a means of

computing the angle between two vectors. For exam-

ple, two two-dimensional vectors a= < a1,a2> and b=

< b1,b2>, with angle θbetween them, form a triangle

in the plane with side-lengths given by the

DISTANCE

FORMULA

: |a| = , |b| = , and |a– b|

=.

By the

LAW OF COSINES

we have:

|a– b|2= |a|2+ |b|2– 2|a||b| cos(θ)

from which it follows that:

a· b= a1b1+ a2b2= |a||b| cos(θ)

Thus the angle between two vectors aand bcan be

computed via the formula:

This formula also holds true for three- and higher-dimen-

sional vectors. For example, consider the unit vector i=

<1,0,0> in three-dimensional space pointing in the direc-

tion of the x-axis, and j= <0,1,0> the corresponding vec-

tor pointing in the direction of the y-axis. As the angle