√(x– c)2+ y2

√(x+ c)2+ y2

160 ellipse

Elizabethan multiplication

Ellipse

the appropriate square cells of the grid as two-digit

entries. (Thus compute 3 ×2 as 06, for example.)

Add the entries in each diagonal starting with the

bottom right diagonal. Write down the units figure and

carry any tens figures that appear to the next diagonal.

The answer, 6,831, now appears along the left column

and bottom row.

This procedure works for multidigit multiplications

of any size. Its success relies on the

DISTRIBUTIVE PROP

-

ERTY

of arithmetic and the process of

EXPANDING

BRACKETS

. In our example,

253 ×27 = (2 ×102+ 5 ×10 + 3) ×(2 ×10 + 7)

= (2 ×2) ×103+ (2 ×7) ×102+ (3 ×2) ×10

+ (5 ×2) ×102+ (5 ×7) ×10

+ 3 ×7

Each diagonal corresponds to a powers-of-10 place,

with entries placed in an upper portion of a square cell

corresponding to carried figures to the next powers-of-

10 position. Try computing a multiplication problem

both the Elizabethan way and the usual way, side-by-

side, to see that the two methods do not differ.

See also E

GYPTIAN MULTIPLICATION

;

FINGER MULTI

-

PLICATION

;

MULTIPLICATION

; N

APIER

’

S BONES

; R

USSIAN

MULTIPLICATION

.

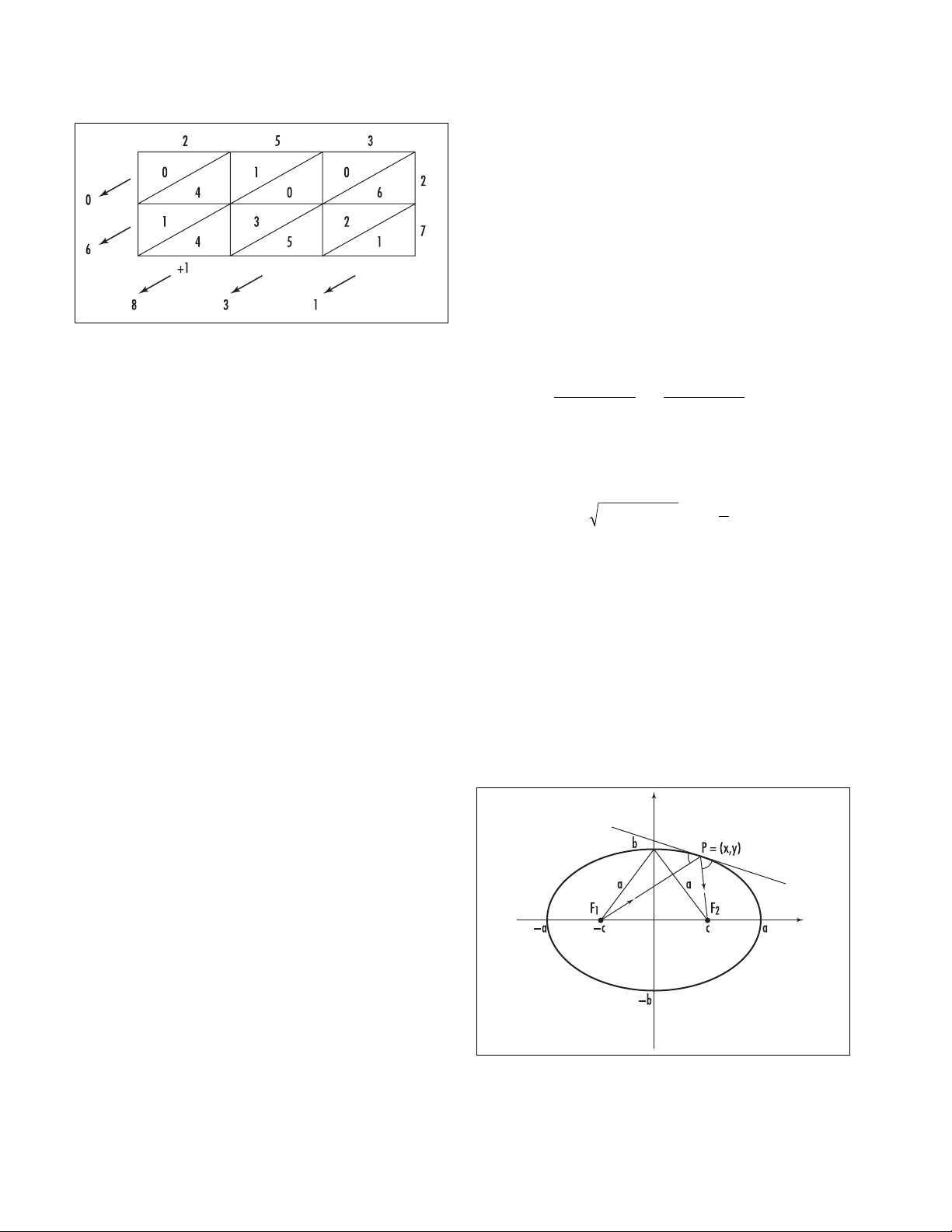
ellipse As one of the

CONIC SECTIONS

, an ellipse is

the plane curve consisting of all points Pwhose dis-

tances from two given points F1and F2in the plane

have a constant sum. The two fixed points F1and F2

are called the foci of the ellipse. An ellipse also arises as

the curve produced by the intersection of a plane with

a single nappe of a right circular

CONE

.

Using the notation |PF1| and |PF2| for the lengths of

the line segments connecting Pto F1and F2, respectively,

the defining condition of an ellipse can be written:

|PF1| + |PF2| = d

where ddenotes the constant sum.

The equation of an ellipse can be found by intro-

ducing a coordinate system in which the foci are

located at positions F1= (–c,0) and F2= (c, 0), for some

positive number c. It is convenient to write d= 2a, for

some a> 0. If P= (x,y) is an arbitrary point on the

ellipse, then the defining condition states:

+ = 2a

Moving the second radical to the right-hand side,

squaring, and simplifying yields the equation:

Squaring and simplifying again yields:

+

Noting that ais greater than c, we can set the positive

quantity a2– c2as equal to b2, for some positive num-

ber b. Thus the equation of the ellipse is:

+ = 1

y2

–

b2

x2

–

a2

= 1

y2

––

a2– c2

x2

–

a2