1

–

n

1

–

n

1

–

n

1

–

n

1

–

3

1

–

2

1

–

n–1

1

–

3

1

–

2

Euler’s formula 175

Understanding Euler’s constant

These statements are proved through a study of the

median of a triangle, the altitude of a triangle, and the

consideration of

EQUIDISTANT

points, respectively.

In the mid-1700s L

EONHARD

E

ULER

(1707–83)

made the astounding discovery that furthermore, for

any triangle, the three points G, H, and Oare

COLLINEAR

, that is, lie on a straight line. This line is

called the Euler line of the triangle.

Euler proved this observation as follows: If, by

chance, the points Oand Gcoincide, then each median

of the triangle is also an altitude. This means that the

triangle is symmetric about each median, and so must

be equilateral. Consequently, the point Hoccurs at the

same location as Oand G, and the three points, triv-

ially, lie on a straight line. If, as is more likely the case,

Oand Gdo not coincide, then draw a line through

them and consider a point Jon this line that is situated

so that the length of the segment GJ is twice that of

OG. Let Mbe the midpoint of the base of the triangle.

From a study of the medians of a triangle, we know

that length of the segment AG to that of GM in the dia-

gram above is in ratio of 2 to 1. Consequently, the two

shaded triangles are similar, and, in particular, angles

AJG and GOM match. By the converse of the

PARALLEL

POSTULATE

, lines OM and AJ are parallel. Since OM

makes an angle of 90°to the base of the triangle, so too

must line AJ, making this line an altitude to the triangle.

Nothing in this argument thus far has relied on

vertex Abeing the object of focus. The same reasoning

shows that the altitude from vertex Balso passes

through the point J, as does the altitude from vertex C.

This shows that the point Jis in fact the orthocenter H

of the triangle. Consequently, O, G, and Hdo indeed

all lie on the same straight line.

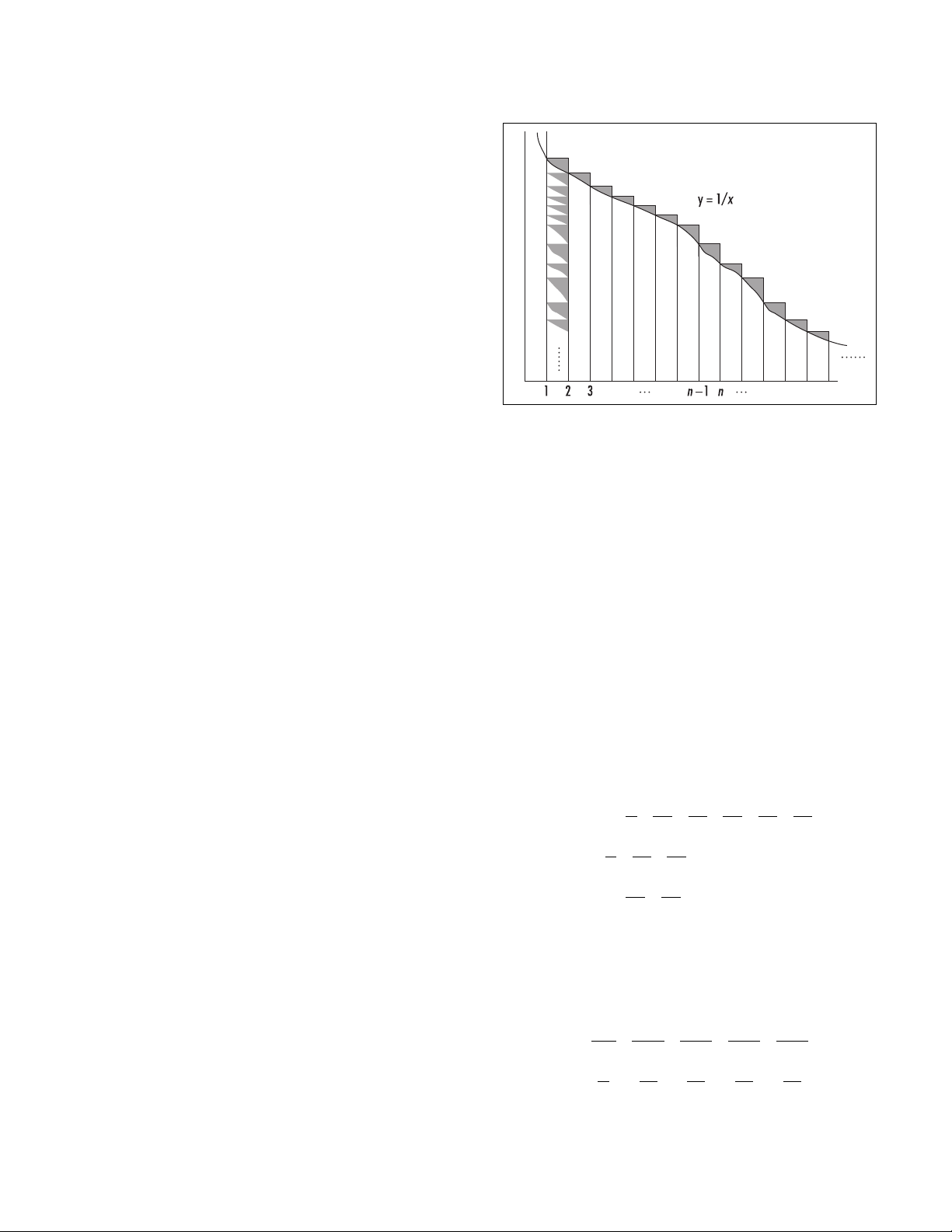
Euler’s constant In drawing rectangles of width 1

that just cover the curve y= 1/x, one sees that the

“excess area” above the curve fits inside the first rect-

angle of height 1, and so sums to a finite value no

larger than 1. The amount of excess area, denoted γ, is

called Euler’s constant. To eight decimal places, it has

value 0.57721566. No one knows whether γis a ratio-

nal or irrational number.

As the area under the curve from x= 1 to x= nis

∫

n

1dx = ln n, we have that 1 + + + … + is

approximately equal to ln(n).More precisely, the sum

of the areas of the first nrectangles is given by:

1 + + + …+ = lnn+ γ+ error

where the “error” is the term minus all the “excess

areas” above the curve from position nonward. Notice

that these excess areas all fit within the rectangle of

height , so this error is no bigger than . In particular,

it is negligibly small if nis large.

See also

HARMONIC SERIES

.

Euler’s formula In 1748 L

EONHARD

E

ULER

noted

that the T

AYLOR SERIES

for the functions ex, sin x, and

cos xare intimately connected. Since

setting x= iθ, where iis the square root of –1 and θis a

real number (usually thought of as an angle), yields: