expected value 179

Computing the product of 23 and 42

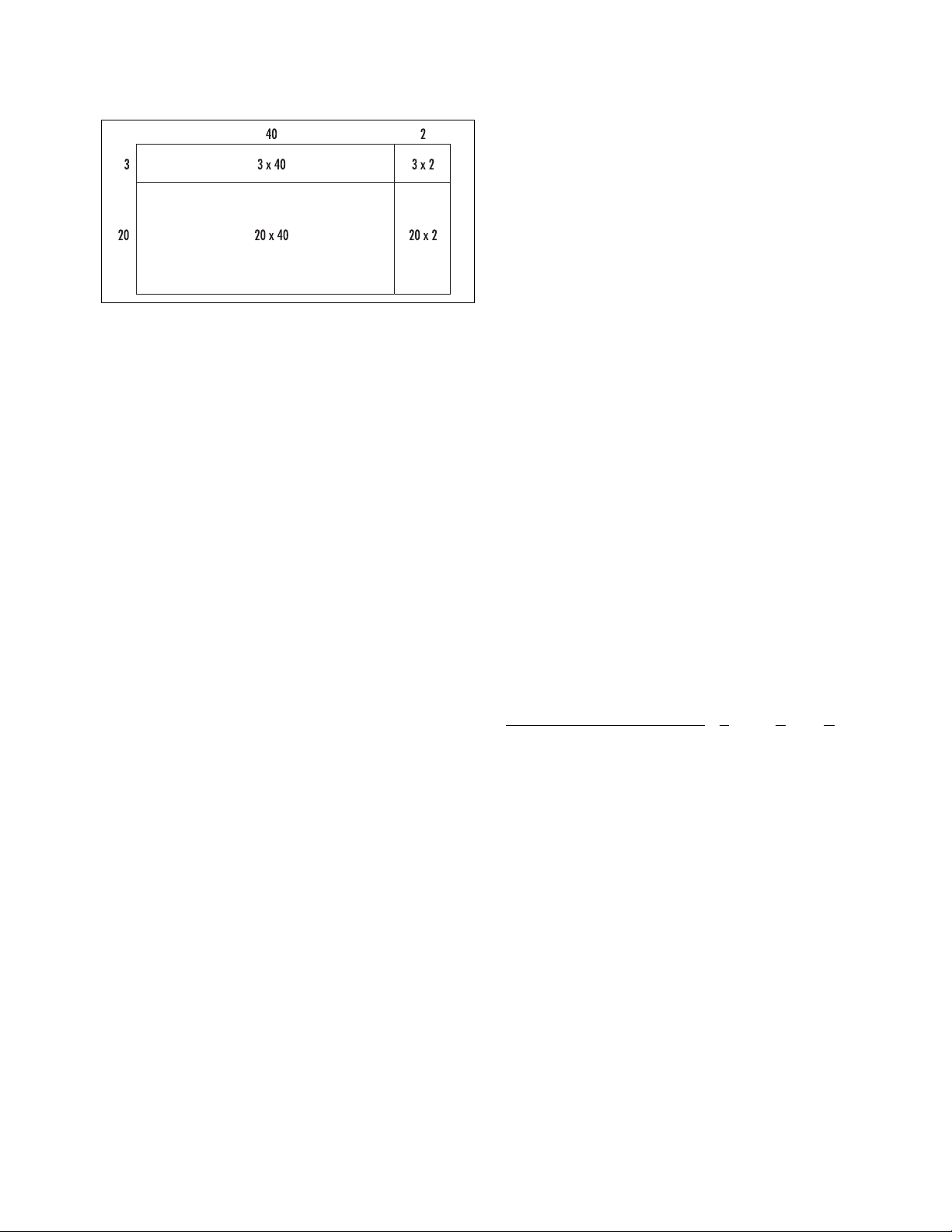
expanding brackets The geometric figure of a rectan-

gle explains the process of expanding brackets. Take, for

example, a 23-by-42 rectangle. Its

AREA

is given by the

product 23 ×42. This product can easily be computed

by thinking of 23 as 20 + 3 and 42 as 40 + 2. This corre-

sponds to subdividing the rectangle into four pieces:

We thus have (20 + 3) ×(40 + 2) = 20 ×40 + 20 ×

2 + 3 ×40 + 3 ×2, which equals 800 + 40 + 120 + 6,

or, 966, which is indeed 23 ×42.

Note that each of the four terms in the sum is the

product of one number in the first set of parentheses

(20 or 3), and one number in the second set (40 and 2),

with all possible pairs of numbers appearing. This prin-

ciple holds in general. For example, the quantity (x+

y)(a+ b+ c) equals the sum of six products: xa + xb +

xc + ya + yb + yc (this corresponds to subdividing a

rectangle into six pieces), and (r+ s+ t+ u+ v)(k+ l+

m+ n+ o+ p+ q) is the sum of 35 individual products.

This principle extends to any number of sets of

parentheses. For example:

(2 + 3) ×(4 + 5) ×(6 + 7) = 2 ×4 ×6 + 2 ×4 ×7 + 2

×5 ×6 + 2 ×5 ×7 + 3 ×4

×6 + 3 ×4 ×7 + 3 ×5 ×6

+ 3 ×5 ×7

(Again select one term from each set of parentheses,

making sure to include all possible combinations.) This

corresponds to subdividing a cube into eight pieces.

It also holds for products containing single terms

along with sets of parentheses. For example, we have:

(a+ b) ×x×(c+ d) = a×x×c+ a×x×d+ b×x×c+

b×x×d.

Many schools teach mnemonic devices for cor-

rectly expanding brackets. These can be more compli-

cated than simply understanding the simple process

at hand.

See also

DISTRIBUTIVE PROPERTY

;

NESTED

MULTIPLICATION

.

expected value (expectation, mean) The expected

value of a game of chance involving monetary bets is

the average or

MEAN

profit (or loss) per game you

would expect if the game were played a large number

of times. The expected value illustrates the extent to

which a game is set to, or against, your favor. To

demonstrate: imagine you have the opportunity to play

the following dice game:

You toss a single die and look at the score cast.

If a 1 comes up you win $10, and if a 2

appears you win $5. If any other number is

cast, you pay a fee of $3 for playing the game.

Is this a game worth playing?

With 600 plays of this game, one would expect

close to one-sixth of those rolls (around 100 of them)

to yield a 1, and hence a gain of $10, another sixth of

the rolls (that is, about 100 rolls) to yield a 2 and a

gain of $5, and two-thirds of the rolls (around 400 of

them) to result in a loss of $3 (that is, a –$3 profit).

The average profit over 600 rolls would thus be:

that is, a gain of 50 cents per game. This positive

expected value shows that the game is indeed worth play-

ing. Note, however, that one might still lose money while

playing the game. What has been demonstrated here is

that, for the long run, the game is set to your favor.

Note the appearance of the fractions 1/6, 1/6, and

4/6 in our computation of expected value. These are

the probabilities of each identified outcome actually

occurring. Such probabilities always appear when com-

puting expected value. In general, if an experiment

yields numerical values x1, x2,…,xn, with pibeing the

probability that outcome xioccurs, then the expected

value of the experiment is given by:

x1p1+ x2p2+…+ xnpn