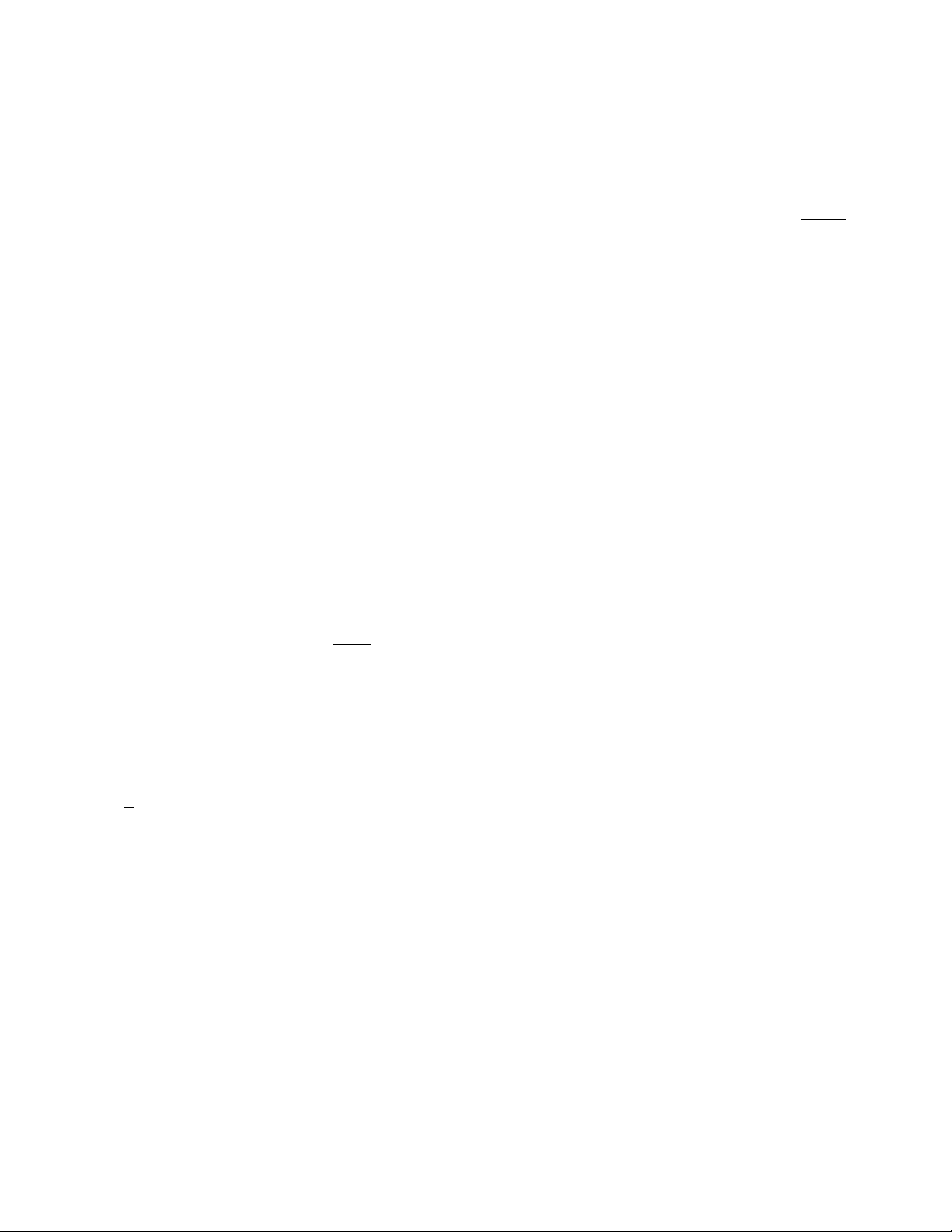
1

––

9

1

––

9

+ ...

1

––

1000

1

––

100

1

––

10

1

––

2

+ ...

1

––

27

1

––

9

1

––

3

224 geometric series

1

––

512

1

––

4

1

––

2

a

––

1 – r

1 – 0

––

1 – r

to Beatrice, and tears the third piece into thirds

again. He hands one piece to Andrea, a second

to Beatrice, and tears the third remaining piece

into thirds again. He repeats this process indef-

initely. Eventually, John will give all the paper

away—half to Andrea and half to Beatrice. But

the quantity of paper Andrea receives and the

quantity Beatrice receives can also be com-

puted as a third, plus a third of a third, plus a

third of a third of a third, and so forth. Thus it

must be the case that + + equals .

A repeating decimal can be thought of as a sum of a

geometric sequence. For example, the decimal 0.111…

equals the series + + , which,

according to the formula above, is . (Consequently the

repeating decimal 0.999… equals 9 times this, 9 ×,

which is 1: 0.999… = 1.)

The sum Sof just the first nterms of a geometric

series, a+ ar + ar2+…+ arn–1 can be computed from the

formula S– rS = a– arn. Provided that r≠1, this gives:

(If –1 < r< 1, then rn→0 as ngrows. This again shows

that a+ ar + ar2+ ar3+ … = a· = .) For

example, the sum 1+ + + … + equals

. A similar calculation solves a

famous “chessboard puzzle”:

Legend has it that the game of chess was

invented for an Indian maharaja who became

so delighted with the game that he wanted to

reward the inventor with whatever he desired.

The inventor asked for nothing more than one

grain of rice on the first square of the chess-

board, two grains on the second square, four

on the third, and so forth, each square contain-

ing double the number of grains than the previ-

ous square. Given that there are 64 squares on

a chessboard, how many grains of rice did the

inventor in fact request?

According to the formula, the inventor asked for 1 + 2

+ 4 + 8 +…+ 263 grains of rice. This equals

= 264 – 1 = 18,446,744,073,709,551,615 grains, which

is the equivalent of about 25 billion cubic miles of rice,

an inconceivable quantity. The inventor fooled the

maharaja into making a promise he could not possibly

honor.

See also

ARITHMETIC SEQUENCE

;

CONVERGENT SE

-

QUENCE

;

SERIES

.

geometric series See

GEOMETRIC SEQUENCE

.

geometric transformation A specified procedure

that shifts points in the plane to different positions

(and thereby changing the location, and possibly the

shapes, of geometric figures) is called a geometric trans-

formation. More precisely, a geometric transformation

is a

FUNCTION

that associates with each point of the

plane some other point in the plane. (One may require

the function to be one-to-one and onto.)

For example, the function that shifts each point of

the plane one unit to the right is a geometric transfor-

mation (called a translation). This transformation pre-

serves the shapes of all geometric figures.

Any geometric transformation that preserves dis-

tances between points in the plane (and hence the

shape and size of geometric figures) is called an isome-

try or a rigid motion. One that multiplies all distances

between points by a constant factor (called the dilation

factor) is called a similitude, and a transformation that

takes straight lines to straight lines is called a

LINEAR

TRANSFORMATION

. All isometries are linear transfor-

mations, for example. These ideas also extend to trans-

formations in three-dimensional space.

While he never made explicit use of the concept in

his writings, the idea of a geometric transformation

came from the work of the Greek geometer E

UCLID

(ca.

300–260

B

.

C

.

E

.).

We list here some classical examples of geometric

transformations.

Reflection in a Line

Given a line lin the plane, a reflection in this line takes

a point Pon one side of lto the corresponding point P′