202 Fourier series

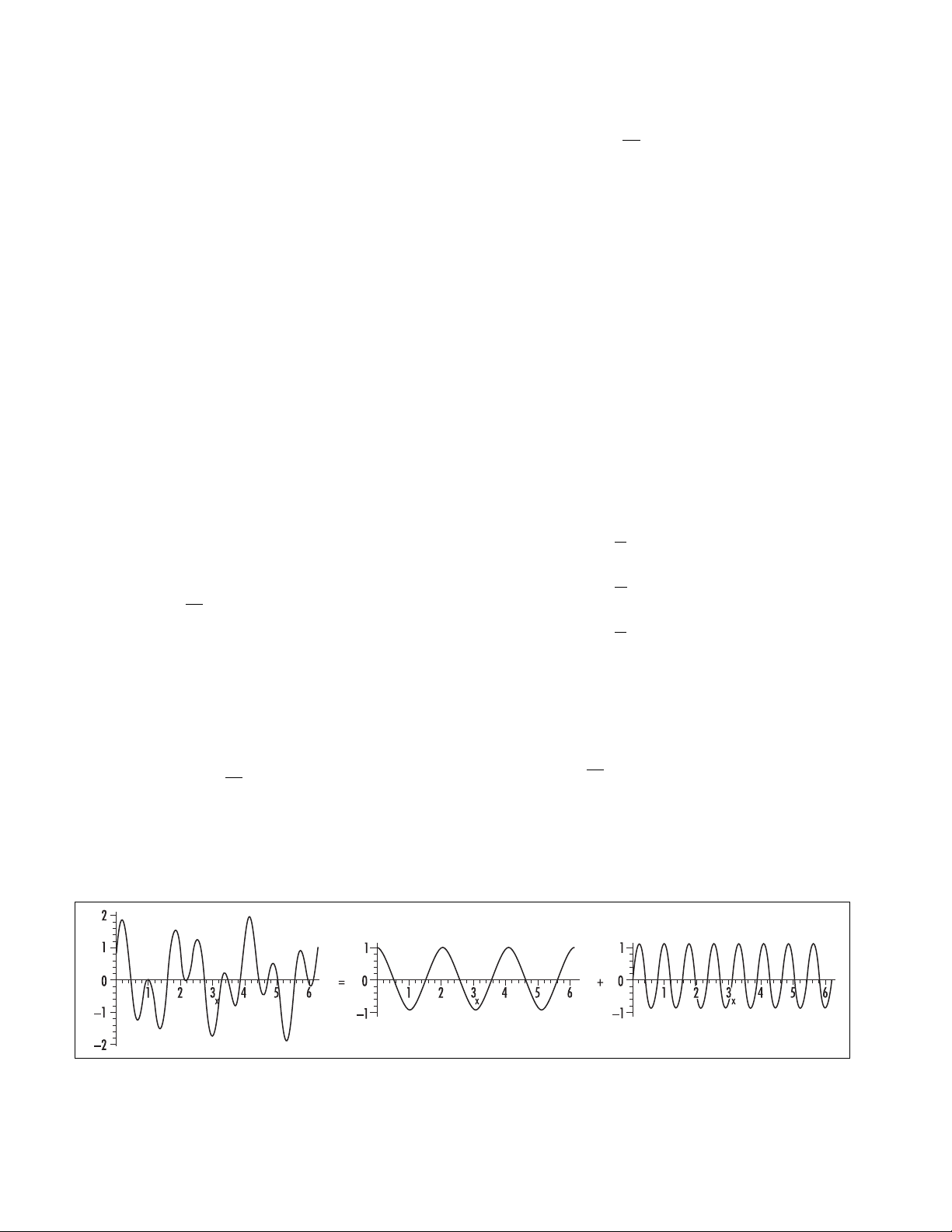
A wave as a sum of a cosine curve and a sine curve

1

–

π

1

–

π

In the 18th century, French mathematician and

physicist J

EAN

L

E

R

OND D

’A

LEMBERT

(1717–83), and

the Swiss mathematician L

EONHARD

E

ULER

(1707–83)

worked to describe complicated vibrations of strings

as sums of simpler functions. The Swiss mathemati-

cian Daniel Bernoulli (1700–82) of the famous

B

ERNOULLI FAMILY

introduced the use of trigonomet-

ric functions in this study, an approach that was later

fully developed by French mathematician and physi-

cist J

EAN

B

APTISTE

J

OSEPH

F

OURIER

(1768–1830),

although his work was motivated by the study of heat

conduction. Fourier showed that many functions

could be represented as infinite sums of sine and

cosine functions.

The result of writing a function as a sum of

trigonometric functions is today called a Fourier series.

As the trigonometric functions cycle in value every 2π

in

RADIAN MEASURE

, it is assumed in these studies that

the functions under consideration are themselves peri-

odic with period 2π.

Assume f(x) is such a function. Then a Fourier

series for fis an expression of the form:

One finds the values of the constants a0,a1,a2,…b1,b2,…

by integrating. For example, since ∫π

–πcos(kx)dx = 0 =

∫π

–πsin(kx)dx, we have:

yielding: a0= ∫π

–πf(x)dx. Multiplying through by

sin(x) and integrating gives:

showing that b1= ∫π

–πf(x)sin(x)dx.

One can show that the functions {1,cos(x),cos(2x),

…,sin(x),sin(2x),…} are

ORTHOGONAL

in the sense that

the integral of the product of any two different func-

tions from this set is zero. This observation allows us

to compute all the values a0,a1,a2,…,b1,b2,… by this

method of multiplying through by a trigonometric

function and integrating. We have, in general:

Mathematicians have shown that if f(x) and its

DERIVATIVE

f′(x) are both

CONTINUOUS FUNCTION

s,

then the expansion

is valid. They have also shown that, if interpreted

appropriately, the expansion remains valid even if for