branch and bound method
A knapsack has maximum weight of 15, and the following items are available: A has weight (w) 5 and value (v) 10, written A (5, 10) with B (7, 11), C (4, 8) and D (4, 12).
Method. Place the items in decreasing order of value per unit weight, i.e. D, A, C, B (A and C could be reversed). Then construct a vector (x1, x2, x3, x4) where xi = 0 if the item is not being taken and xi = 1 if it is. Start with (0, 0, 0, 0). At each stage, if a branch has not been terminated, and there are n zeros at the end of the vector, construct n branches which change exactly one of those zeros to a one and for which the total weight does not exceed the limit so the first stage will have four branches (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) and (0, 0, 0, 1). Calculate the total weight (w) for each new branch created, and the value (v), and repeat the process.
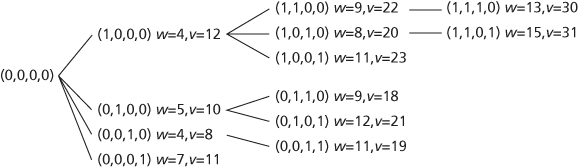
Example illustrating the branch and bound method
From the figure we see that the optimal solution is to choose items B, C, D with total weight 15 and value 31.
- soluble group
- solution
- solution of triangles
- solution set
- solvable by radicals
- solvable group
- sorting algorithms
- source
- source
- source
- space
- space-filling curve
- space–time
- span
- spanning set
- spanning tree
- sparse matrix
- Spearman's rank correlation coefficient
- special function
- special linear group
- special relativity
- spectral theorem
- spectrum
- speed
- speed of light