differentiable function
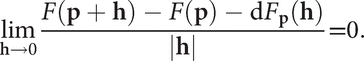
dFp is known as the differential (or derivative) of F at p. When m = n = 1, then dFp is a 1×1 matrix with entry F'(p). More generally dFp is represented by the Jacobian matrix at p. A function F:Rn→Rm can be expanded as
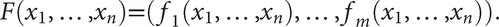
It is sufficient for F to be differentiable for all the partial derivatives ∂fi/∂xj to exist and be continuous (see continuous function). More generally, for a differentiable function F:M → N between smooth manifolds M and N, the differential at p in M is a linear map dFp:Tp(M) → TF(p)(N) between tangent spaces. For v in Tp(M) take a curve γ in M such that γ(0) = p and γ' (0) = v. Then F(γ) is a curve in N and dFp(v) = (F◦γ)' (0).