gradient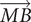
where the line through M and B has positive direction upwards. In other words, MB equals the length |MB| if B is above M, and equals −|MB| if B is below M. Similarly, AM = −|AM| if M is to the right of A, and AM = −|AM| if M is to the left of A. Two cases are illustrated in the figures.)
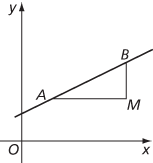
B is above A
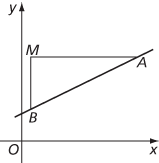
B is below A
The gradient of the line through A and B may be denoted by mAB, and, if A and B have coordinates (x1, y1) and (x2, y2), with x1 ≠ x2, then
Though defined in terms of two points A and B on the line, the gradient of the line is independent of the choice of A and B. The line in the figures has gradient 
.
Alternatively, the gradient may be defined as equal to tanθ, where either direction of the line makes an angle θ with the positive x‐axis. (The different possible values for θ give the same value for tanθ.) If the line through A and B is vertical, that is, parallel to the y‐axis, it is customary to say that the gradient is infinite. The following properties hold:
- Dirac delta function
- Dirac, Paul Adrien Maurice
- directed graph
- directed line
- directed line segment
- directed number
- direction
- directional data
- directional derivative
- direction angles
- direction cosines
- direction fields
- direction ratios
- direct isometry
- directly proportional
- direct product
- direct proof
- directrix
- direct sum
- direct variation
- Dirichlet beta function
- Dirichlet function
- Dirichlet, Peter Gustav Lejeune
- Dirichlet problem
- Dirichlet's approximation theorem