| 释义 |
limit (of a sequence) Informally, the limit, if it exists, of an infinite real sequence a1, a2, a3,…is a number l with the property that an gets closer to l as n gets indefinitely large.
More precisely, the sequence a1, a2, a3,…has the limit l if, given any ε > 0 (however small), there is a number N (which may depend on ε) such that, for all n>N, an lies between l−ε and l + ε. This is written an → l. A sequence's limit, if it exists, is unique. For example, the sequence 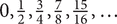 , has limit 1, and the sequence , has limit 1, and the sequence 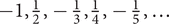 has the limit 0; since this is the sequence whose nth term is (−1)n/n; this fact can be stated as (−1)n/n → 0. has the limit 0; since this is the sequence whose nth term is (−1)n/n; this fact can be stated as (−1)n/n → 0. There are, of course, real sequences that do not have a limit. These can be classified into different kinds. (i) an tends to ∞, written an → ∞ if, given any K (however large), there is an integer N (which may depend on K) such that, for all n>N, an>K. For example, an → ∞ for the sequence an = n2. (ii) There is a similar definition for an →−∞, and an example is the sequence −4,−5,−6,…, in which an = −n−3. (iii) The sequence does not have a limit but is bounded, such as the sequence  , in which an = (−1) n n/(n + 1). (iv) The sequence is not bounded, but it is not the case that an → ∞ or an →−∞. The sequence 1, 2, 1, 4, 1, 8, 1,…is an example.If a sequence an converges to l, then all subsequences of an also converge to l.More generally, a sequence an in a metric space M converges to a limit l if d(an,l) → 0 as n → ∞. Thus a complex sequence (see complex number) an converges to the complex number l if |an – l|→ 0 as n → ∞. This is equivalent to Re(an) → Re(l) and Im(an) → Im(l).Sequential convergence determines the topology of a metric space, in the sense that a point x is in the closure of a set A if there exists a sequence an in A which converges to x. This is not true more generally in topological spaces.See algebra of limits, Bolzano-Weierstrass theorem. |
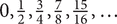 , has limit 1, and the sequence
, has limit 1, and the sequence 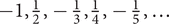 has the limit 0; since this is the sequence whose nth term is (−1)n/n; this fact can be stated as (−1)n/n → 0.
has the limit 0; since this is the sequence whose nth term is (−1)n/n; this fact can be stated as (−1)n/n → 0. , in which an = (−1)n n/(n + 1).
, in which an = (−1)n n/(n + 1).