| 释义 |
Population GrowthThe differential equation describing exponential growth is
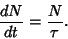 | (1) |
 | (2) |
 | (3) |
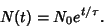 | (4) |
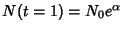 gives gives  in (4), so in (4), so
 | (5) |
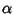 in this equation is sometimes known as the Malthusian Parameter. in this equation is sometimes known as the Malthusian Parameter.
Consider a more complicated growth law
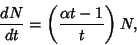 | (6) |
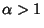 is a constant. This can also be integrated directly is a constant. This can also be integrated directly
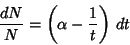 | (7) |
 | (8) |
 | (9) |
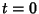 . We are given the Initial Conditionthat . We are given the Initial Conditionthat 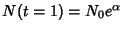 , so , so 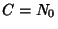 . .
 | (10) |
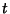 in the Denominator of (10) greatly suppresses the growth in the long runcompared to the simple growth law. in the Denominator of (10) greatly suppresses the growth in the long runcompared to the simple growth law.
The Logistic Growth Curve, defined by
 | (11) |
 .See also Gompertz Curve, Life Expectancy, Logistic Growth Curve, Lotka-Volterra Equations,Makeham Curve, Malthusian Parameter, Survivorship Curve .See also Gompertz Curve, Life Expectancy, Logistic Growth Curve, Lotka-Volterra Equations,Makeham Curve, Malthusian Parameter, Survivorship Curve
|