Block Growth

Let be a sequence over a finite Alphabet (all the entries are elements of ). Definethe block growth function of a sequence to be the number of Admissible words of length . For example, inthe sequence ..., the following words are Admissible

Length	Admissible Words
1
2
3
4

so , , , , and so on. Notice that , so the block growth function isalways nondecreasing. This is because any Admissible word of length can be extended rightwards to produce anAdmissible word of length . Moreover, suppose for some . Then each admissible word oflength extends to a unique Admissible word of length .

For a Sequence in which each substring of length uniquely determines the next symbol in theSequence, there are only finitely many strings of length , so the process must eventually cycle and theSequence must be eventually periodic. This gives us the following theorems:

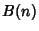1. If the Sequence is eventually periodic, with least period , then is strictly increasing until itreaches , and 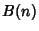is constant thereafter.

2. If the Sequence is not eventually periodic, then 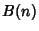is strictly increasing and so 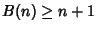for all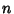. If a Sequence has the property that for all 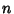, then it is said to have minimal block growth, and theSequence is called a Sturmian Sequence.

The block growth is also called the Growth Function or the Complexity of aSequence.

• Semimagic Square
• Semimajor Axis
• Semiminor Axis
• Semiperfect Magic Cube
• Semiperfect Number
• Semiperimeter
• Semiprime
• Semiprime Ring
• Semiregular Polyhedron
• Semiring
• Andrews-Curtis Link
• Andrews-Schur Identity
• Andrew's Sine
• Andrica's Conjecture
• André's Problem
• André's Reflection Method
• Anger Function
• Angle
• Angle Bisector
• Angle Bisector Theorem
• Angle Bracket
• Angle of Parallelism
• Angle Trisection
• Angular Acceleration
• Angular Defect