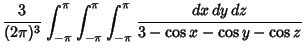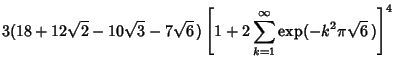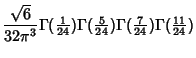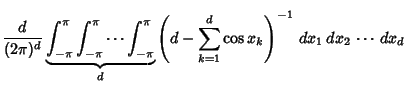| 释义 |
Pólya's Random Walk ConstantsN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Let 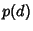 be the probability that a Random Walk on a be the probability that a Random Walk on a 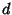 -D lattice returns to the origin. Pólya (1921) provedthat -D lattice returns to the origin. Pólya (1921) provedthat
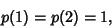 | (1) |
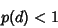 | (2) |
 . Watson (1939), McCrea and Whipple (1940), Domb (1954), and Glasser and Zucker (1977) showed that . Watson (1939), McCrea and Whipple (1940), Domb (1954), and Glasser and Zucker (1977) showed that
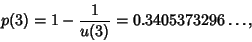 | (3) |
where 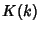 is a complete Elliptic Integral of the First Kind and is a complete Elliptic Integral of the First Kind and 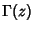 is the Gamma Function. Closedforms for is the Gamma Function. Closedforms for 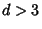 are not known, but Montroll (1956) showed that are not known, but Montroll (1956) showed that
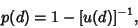 | (9) |
and 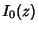 is a Modified Bessel Function of the First Kind. Numerical values from Montroll (1956) and Flajolet(Finch) are is a Modified Bessel Function of the First Kind. Numerical values from Montroll (1956) and Flajolet(Finch) are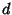 | 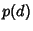 | | 4 | 0.20 | | 5 | 0.136 | | 6 | 0.105 | | 7 | 0.0858 | | 8 | 0.0729 |
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/polya/polya.htmlDomb, C. ``On Multiple Returns in the Random-Walk Problem.'' Proc. Cambridge Philos. Soc. 50, 586-591, 1954. Glasser, M. L. and Zucker, I. J. ``Extended Watson Integrals for the Cubic Lattices.'' Proc. Nat. Acad. Sci. U.S.A. 74, 1800-1801, 1977. McCrea, W. H. and Whipple, F. J. W. ``Random Paths in Two and Three Dimensions.'' Proc. Roy. Soc. Edinburgh 60, 281-298, 1940. Montroll, E. W. ``Random Walks in Multidimensional Spaces, Especially on Periodic Lattices.'' J. SIAM 4, 241-260, 1956. Watson, G. N. ``Three Triple Integrals.'' Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939. |
![]() be the probability that a Random Walk on a
be the probability that a Random Walk on a ![]() -D lattice returns to the origin. Pólya (1921) provedthat
-D lattice returns to the origin. Pólya (1921) provedthat