| 释义 |
Quadratic MapA 1-D Map often called ``the'' quadratic map is defined by
 | (1) |
 , and repelling if , and repelling if 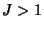 . Fixed Points occur when . Fixed Points occur when
 | (2) |
 | (3) |
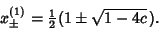 | (4) |
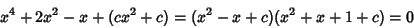 | (6) |
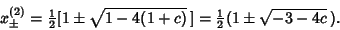 | (7) |
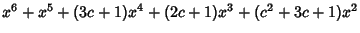 | | 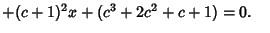 | (8) |
The most general second-order 2-D Map with an elliptic fixed point at the origin has the form
The map must have a Determinant of 1 in order to be Area preserving, reducing the number of independent parameters from seven to three. The map can then be put in a standard form by scaling and rotating to obtain
The inverse map is
The Fixed Points are given by
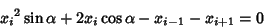 | (15) |
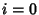 , ..., , ...,  .See also Bogdanov Map, Hénon Map, Logistic Map, Lozi Map, Mandelbrot Set .See also Bogdanov Map, Hénon Map, Logistic Map, Lozi Map, Mandelbrot Set |