| 释义 |
Area PrincipleThe ``Area principle'' states that
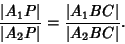 | (1) |
 | (2) |
 | (3) |
 and and  for for 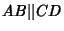 with a Plus or Minus Signdepending on if these segments have the same or opposite directions, and with a Plus or Minus Signdepending on if these segments have the same or opposite directions, and
 | (4) |
References
Grünbaum, B. and Shepard, G. C. ``Ceva, Menelaus, and the Area Principle.'' Math. Mag. 68, 254-268, 1995.
|
