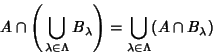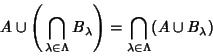| 释义 |
SetA set is a Finite or Infinite collection of objects. Older words for set include Aggregate andClass. Russell also uses the term Manifold to refer to a set. The study of sets and theirproperties is the object of Set Theory. Symbols used to operate on sets include 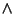 (which denotes theEmpty Set (which denotes theEmpty Set 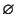 ), ), 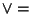 (which denotes the Power Set of a set), (which denotes the Power Set of a set), 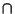 (which means ``and'' orIntersection), and (which means ``and'' orIntersection), and 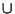 (which means ``or'' or Union). (which means ``or'' or Union).
The Notation 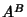 , where , where  and and 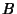 are arbitrary sets, is used to denote the set of Maps from are arbitrary sets, is used to denote the set of Maps from 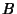 to to . For example, an element of . For example, an element of 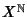 would be a Map from the Natural Numbers would be a Map from the Natural Numbers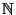 to the set to the set  . Call such a function . Call such a function 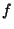 , then , then  , , 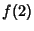 , etc., are elements of , etc., are elements of  , so call them , so call them  , ,  ,etc. This now looks like a Sequence of elements of ,etc. This now looks like a Sequence of elements of  , so sequences are really just functions from , so sequences are really just functions from 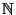 to to  . This Notation is standard in mathematics and is frequently used in symbolic dynamics to denote sequence spaces. . This Notation is standard in mathematics and is frequently used in symbolic dynamics to denote sequence spaces.
Let 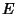 , ,  , and , and 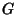 be sets. Then operation on these sets using the be sets. Then operation on these sets using the 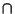 and and 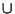 operators is Commutative operators is Commutative
 | (1) |
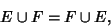 | (2) |
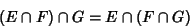 | (3) |
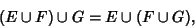 | (4) |
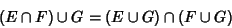 | (5) |
 | (6) |
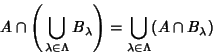 | (7) |
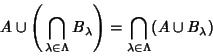 | (8) |
 runs through any Index Set runs through any Index Set 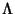 . The proofs follow trivially from the definitions of union andintersection. . The proofs follow trivially from the definitions of union andintersection.
The table below gives symbols for some common sets in mathematics.
| Symbol | Set |  | 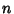 -Ball -Ball | 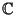 | Complex Numbers | 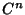 , , 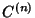 | 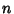 -Differentiable Functions -Differentiable Functions | 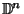 | 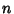 -Disk -Disk | 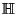 | Quaternions | 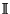 | Integers | 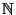 | Natural Numbers | 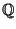 | Rational Numbers |  | Real Numbers in 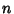 -D -D |  | 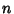 -Sphere -Sphere | 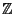 | Integers |  | integers (mod 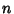 ) ) | 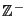 | Negative Integers | 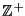 | Positive Integers | 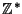 | Nonnegative Integers |
References
Courant, R. and Robbins, H. ``The Algebra of Sets.'' Supplement to Ch. 2 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 108-116, 1996.
|
![]() (which denotes theEmpty Set
(which denotes theEmpty Set ![]() ),
), ![]() (which denotes the Power Set of a set),
(which denotes the Power Set of a set), ![]() (which means ``and'' orIntersection), and
(which means ``and'' orIntersection), and ![]() (which means ``or'' or Union).
(which means ``or'' or Union).![]() , where
, where ![]() and
and ![]() are arbitrary sets, is used to denote the set of Maps from
are arbitrary sets, is used to denote the set of Maps from ![]() to
to![]() . For example, an element of
. For example, an element of ![]() would be a Map from the Natural Numbers
would be a Map from the Natural Numbers![]() to the set
to the set ![]() . Call such a function
. Call such a function ![]() , then
, then ![]() ,
, ![]() , etc., are elements of
, etc., are elements of ![]() , so call them
, so call them ![]() ,
, ![]() ,etc. This now looks like a Sequence of elements of
,etc. This now looks like a Sequence of elements of ![]() , so sequences are really just functions from
, so sequences are really just functions from ![]() to
to ![]() . This Notation is standard in mathematics and is frequently used in symbolic dynamics to denote sequence spaces.
. This Notation is standard in mathematics and is frequently used in symbolic dynamics to denote sequence spaces.![]() ,
, ![]() , and
, and ![]() be sets. Then operation on these sets using the
be sets. Then operation on these sets using the ![]() and
and ![]() operators is Commutative
operators is Commutative