| 释义 |
PiA Real Number denoted  which is defined as the ratio of a Circle's Circumference which is defined as the ratio of a Circle's Circumference  to itsDiameter to itsDiameter  , ,
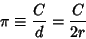 | (1) |
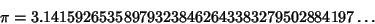 | (2) |
 has recently (August 1997) been computed to a world record has recently (August 1997) been computed to a world record  Decimal Digits by Y. Kanada. This calculation was done using Borwein's fourth-order convergentalgorithm and required 29 hours on a massively parallel 1024-processor Hitachi SR2201 supercomputer. It was checked in 37hours using the Brent-Salamin Formula on the same machine. Decimal Digits by Y. Kanada. This calculation was done using Borwein's fourth-order convergentalgorithm and required 29 hours on a massively parallel 1024-processor Hitachi SR2201 supercomputer. It was checked in 37hours using the Brent-Salamin Formula on the same machine.
The Simple Continued Fraction for  , which gives the ``best'' approximation of a given order, is [3, 7, 15, 1, 292, 1, 1,1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, ...] (Sloane's A001203). The very large term 292 means that the Convergent , which gives the ``best'' approximation of a given order, is [3, 7, 15, 1, 292, 1, 1,1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, ...] (Sloane's A001203). The very large term 292 means that the Convergent
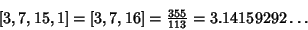 | (3) |
 in the ContinuedFraction are 4, 9, 1, 30, 40, 32, 2, 44, 130, 100, ... (Sloane's A032523). in the ContinuedFraction are 4, 9, 1, 30, 40, 32, 2, 44, 130, 100, ... (Sloane's A032523).
Gosper has computed 17,001,303 terms of  's Continued Fraction (Gosper 1977, Ball and Coxeter 1987), although thecomputer on which the numbers are stored may no longer be functional (Gosper, pers. comm., 1998). According to Gosper, atypical Continued Fraction term carries only slightly more significance than a decimal Digit. The sequence ofincreasing terms in the A033089), occurring at positions1, 2, 3, 5, 308, 432, ... (Sloane's A033090). In the first 26,491 terms of the Continued Fraction (counting 3 as the0th), the only five-Digit terms are 20,776 (the 431st), 19,055 (15,543rd), and 19,308 (23,398th) (Beeler et al. 1972,Item 140). The first 6-Digit term is 528,210 (the 267,314th), and the first 8-Digit term is 12,996,958(453,294th). The term having the largest known value is the whopping 9-Digit 87,878,3625 (the 11,504,931st term). 's Continued Fraction (Gosper 1977, Ball and Coxeter 1987), although thecomputer on which the numbers are stored may no longer be functional (Gosper, pers. comm., 1998). According to Gosper, atypical Continued Fraction term carries only slightly more significance than a decimal Digit. The sequence ofincreasing terms in the A033089), occurring at positions1, 2, 3, 5, 308, 432, ... (Sloane's A033090). In the first 26,491 terms of the Continued Fraction (counting 3 as the0th), the only five-Digit terms are 20,776 (the 431st), 19,055 (15,543rd), and 19,308 (23,398th) (Beeler et al. 1972,Item 140). The first 6-Digit term is 528,210 (the 267,314th), and the first 8-Digit term is 12,996,958(453,294th). The term having the largest known value is the whopping 9-Digit 87,878,3625 (the 11,504,931st term).
The Simple Continued Fraction for  does not show any obvious patterns, but clear patterns do emerge in thebeautiful non-simple Continued Fractions does not show any obvious patterns, but clear patterns do emerge in thebeautiful non-simple Continued Fractions
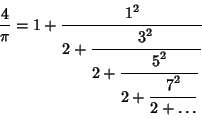 | (4) |
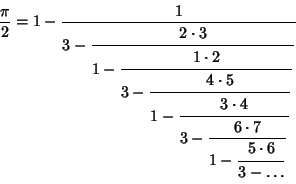 | (5) |
 crops up in all sorts of unexpected places in mathematics besides Circles and Spheres. For example, it occurs in the normalization of the Gaussian Distribution, in the distribution of Primes,in the construction of numbers which are very close to Integers (the Ramanujan Constant),and in the probability that a pin dropped on a set of Parallel lines intersects a line (Buffon's NeedleProblem). Pi also appears as the average ratio of the actual length and the direct distance between source and mouth in ameandering river (Stéllum 1996, Singh 1997). crops up in all sorts of unexpected places in mathematics besides Circles and Spheres. For example, it occurs in the normalization of the Gaussian Distribution, in the distribution of Primes,in the construction of numbers which are very close to Integers (the Ramanujan Constant),and in the probability that a pin dropped on a set of Parallel lines intersects a line (Buffon's NeedleProblem). Pi also appears as the average ratio of the actual length and the direct distance between source and mouth in ameandering river (Stéllum 1996, Singh 1997).
A brief history of Notation for pi is given by Castellanos (1988).  is sometimes known as Ludolph's Constantafter Ludolph van Ceulen (1539-1610), a Dutch is sometimes known as Ludolph's Constantafter Ludolph van Ceulen (1539-1610), a Dutch  calculator. The symbol calculator. The symbol  was first used by William Jones in 1706, andsubsequently adopted by Euler. was first used by William Jones in 1706, andsubsequently adopted by Euler.  In Measurement of a Circle, Archimedes In Measurement of a Circle, Archimedes  (ca. 225BC (ca. 225BC  ) obtained the first rigorous approximation by Inscribing andCircumscribing ) obtained the first rigorous approximation by Inscribing andCircumscribing  -gons on a Circle using the Archimedes Algorithm. Using -gons on a Circle using the Archimedes Algorithm. Using 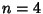 (a 96-gon), Archimedes (a 96-gon), Archimedes  obtained obtained
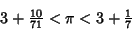 | (6) |
The Bible contains two references (I Kings 7:23 and Chronicles 4:2) which give a value of 3 for  . It should bementioned, however, that both instances refer to a value obtained from physical measurements and, as such, are probablywell within the bounds of experimental uncertainty. I Kings 7:23 states, ``Also he made a molten sea of tenCubits . It should bementioned, however, that both instances refer to a value obtained from physical measurements and, as such, are probablywell within the bounds of experimental uncertainty. I Kings 7:23 states, ``Also he made a molten sea of tenCubits  from brim to brim, round in compass, and five cubits in height thereof; and a line thirtycubits did compass it round about.'' This implies from brim to brim, round in compass, and five cubits in height thereof; and a line thirtycubits did compass it round about.'' This implies 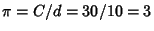 . The Babylonians gave an estimate of . The Babylonians gave an estimate of  as as 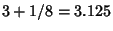 . The Egyptians did better still, obtaining . The Egyptians did better still, obtaining 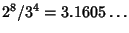 in the Rhind papyrus, and 22/7 elsewhere. TheChinese geometers, however, did best of all, rigorously deriving in the Rhind papyrus, and 22/7 elsewhere. TheChinese geometers, however, did best of all, rigorously deriving  to 6 decimal places. to 6 decimal places.
A method similar to Archimedes'  can be used to estimate can be used to estimate  by starting with an by starting with an  -gon and thenrelating the Area of subsequent -gon and thenrelating the Area of subsequent  -gons. Let -gons. Let 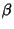 be the Angle from the center of one of thePolygon's segments, be the Angle from the center of one of thePolygon's segments,
 | (7) |
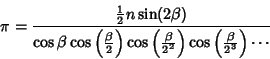 | (8) |
 by taking by taking 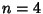 in theabove expression, giving in theabove expression, giving
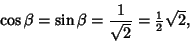 | (9) |
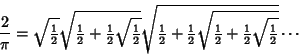 | (10) |
 | (11) |
 and the and the  th Prime th Prime  is is
(Blatner 1997, p. 119), plotted below as a function of the number of terms in the product.
The Area and Circumference of the Unit Circle are given by
and
The Surface Area and Volume of the unit Sphere are
 is known to be Irrational (Lambert 1761, Legendre 1794) and evenTranscendental (Lindemann 1882). Incidentally, Lindemann's proof of the transcendence of is known to be Irrational (Lambert 1761, Legendre 1794) and evenTranscendental (Lindemann 1882). Incidentally, Lindemann's proof of the transcendence of also proved that the Geometric Problem of Antiquity known as CircleSquaring is impossible. A simplified, but still difficult, version of Lindemann's proof is given by Klein (1955). also proved that the Geometric Problem of Antiquity known as CircleSquaring is impossible. A simplified, but still difficult, version of Lindemann's proof is given by Klein (1955).
It is also known that  is not a Liouville Number (Mahler 1953). In 1974, M. Mignotte showed that is not a Liouville Number (Mahler 1953). In 1974, M. Mignotte showed that
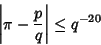 | (20) |
 | (21) |
 , where , where  is an infinitesimally small number(Borwein et al. 1989). It is not known if is an infinitesimally small number(Borwein et al. 1989). It is not known if  is Normal (Wagon 1985), although the first 30million Digits are very Uniformly Distributed (Bailey 1988). The followingdistribution is found for the first is Normal (Wagon 1985), although the first 30million Digits are very Uniformly Distributed (Bailey 1988). The followingdistribution is found for the first  Digits of Digits of 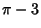 . It shows no statisticallySignificant departure from a Uniform Distribution (technically, in the Chi-Squared Test, ithas a value of . It shows no statisticallySignificant departure from a Uniform Distribution (technically, in the Chi-Squared Test, ithas a value of  for the first for the first  terms). terms).
| digit | 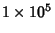 |  | 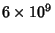 |  | | 0 | 9,999 | 99,959 | 599,963,005 | 5,000,012,647 | | 1 | 10,137 | 99,758 | 600,033,260 | 4,999,986,263 | | 2 | 9,908 | 100,026 | 599,999,169 | 5,000,020,237 | | 3 | 10,025 | 100,229 | 600,000,243 | 4,999,914,405 | | 4 | 9,971 | 100,230 | 599,957,439 | 5,000,023,598 | | 5 | 10,026 | 100,359 | 600,017,176 | 4,999,991,499 | | 6 | 10,029 | 99,548 | 600,016,588 | 4,999,928,368 | | 7 | 10,025 | 99,800 | 600,009,044 | 5,000,014,860 | | 8 | 9,978 | 99,985 | 599,987,038 | 5,000,117,637 | | 9 | 9,902 | 100,106 | 600,017,038 | 4,999,990,486 |
The digits of 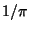 are also very uniformly distributed ( are also very uniformly distributed (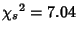 ), as shown in the following table. ), as shown in the following table. | digit |  | | 0 | 4,999,969,955 | | 1 | 5,000,113,699 | | 2 | 4,999,987,893 | | 3 | 5,000,040,906 | | 4 | 4,999,985,863 | | 5 | 4,999,977,583 | | 6 | 4,999,990,916 | | 7 | 4,999,985,552 | | 8 | 4,999,881,183 | | 9 | 5,000,066,450 |
It is not known if 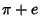 , ,  , or , or  are Irrational. However, it is known that theycannot satisfy any Polynomial equation of degree are Irrational. However, it is known that theycannot satisfy any Polynomial equation of degree 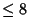 with Integer Coefficients ofaverage size 109 (Bailey 1988, Borwein et al. 1989). with Integer Coefficients ofaverage size 109 (Bailey 1988, Borwein et al. 1989).
 satisfies the Inequality satisfies the Inequality
 | (22) |
Beginning with any Positive Integer  , round up to the nearest multiple of , round up to the nearest multiple of 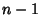 , then up to the nearest multipleof , then up to the nearest multipleof 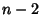 , and so on, up to the nearest multiple of 1. Let , and so on, up to the nearest multiple of 1. Let  denote the result. Then the ratio denote the result. Then the ratio
 | (23) |
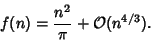 | (24) |
 are 1, 2, 4, 6, 10, 12, 18, 22, 30, 34, ... (Sloane's A002491). are 1, 2, 4, 6, 10, 12, 18, 22, 30, 34, ... (Sloane's A002491).
A particular case of the Wallis Formula gives
 | (25) |
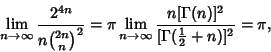 | (26) |
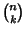 denotes a Binomial Coefficient and denotes a Binomial Coefficient and  is the Gamma Function (Knopp 1990).Euler is the Gamma Function (Knopp 1990).Euler  obtained obtained
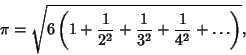 | (27) |
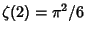 . SimilarFormulas follow from . SimilarFormulas follow from  for all Positive Integers for all Positive Integers  . Gregory . Gregory  and Leibniz and Leibniz  found found
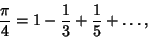 | (28) |
 th term of this series in Gregory's Formulais larger than th term of this series in Gregory's Formulais larger than  so this sum converges so slowly that 300 terms are not sufficient to calculate so this sum converges so slowly that 300 terms are not sufficient to calculate  correctly totwo decimal places! However, it can be transformed to correctly totwo decimal places! However, it can be transformed to
 | (29) |
 is the Riemann Zeta Function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the errorafter is the Riemann Zeta Function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the errorafter  terms is terms is 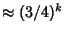 . Newton . Newton  used used
(Borwein et al. 1989). Using Euler's  Convergence Improvement transformation gives Convergence Improvement transformation gives
(Beeler et al. 1972, Item 120). This corresponds to plugging 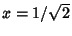 into the Power Series for theHypergeometric Function into the Power Series for theHypergeometric Function  , ,
 | (34) |
 gives 2 bits/term, gives 2 bits/term,
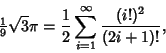 | (35) |
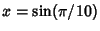 gives almost 3.39 bits/term, gives almost 3.39 bits/term,
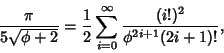 | (36) |
 is the Golden Ratio. Gosper also obtained is the Golden Ratio. Gosper also obtained
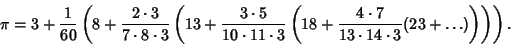 | (37) |
 is is
 | (38) |
 (1913-14), (1913-14),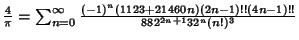 | | | (39) |
and
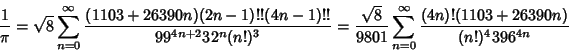 | (40) |
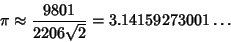 | (41) |
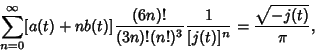 | (42) |
 is a Quadratic Form Discriminant, is a Quadratic Form Discriminant,  is the j-Function, is the j-Function,
and the  are Ramanujan-Eisenstein Series. A Class Number are Ramanujan-Eisenstein Series. A Class Number  field involves field involves  th degree AlgebraicIntegers of the constants th degree AlgebraicIntegers of the constants  , ,  , and , and  . The fastest converging series that uses onlyInteger terms corresponds to the largest Class Number 1 discriminant of . The fastest converging series that uses onlyInteger terms corresponds to the largest Class Number 1 discriminant of 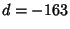 and was formulated by theChudnovsky brothers (1987). The 163 appearing here is the same one appearing in the fact that and was formulated by theChudnovsky brothers (1987). The 163 appearing here is the same one appearing in the fact that 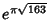 (theRamanujan Constant) is very nearly an Integer. The series is given by (theRamanujan Constant) is very nearly an Integer. The series is given by
(Borwein and Borwein 1993). This series gives 14 digits accurately per term. The same equation in another form was given by the Chudnovsky brothers (1987) and is used by Mathematica (Wolfram Research,Champaign, IL) to calculate (Wolfram Research,Champaign, IL) to calculate  (Vardi 1991), (Vardi 1991),
 | (46) |
The best formula for Class Number 2 (largest discriminant 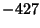 ) is ) is
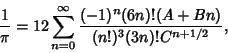 | (50) |
(Borwein and Borwein 1993). This series adds about 25 digits for each additional term. The fastest converging seriesfor Class Number 3 corresponds to 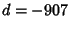 and gives 37-38 digits per term. The fastest converging ClassNumber 4 series corresponds to and gives 37-38 digits per term. The fastest converging ClassNumber 4 series corresponds to  and is and is
 | (54) |
This gives 50 digits per term. Borwein and Borwein (1993) have developed a general Algorithm for generating suchseries for arbitrary Class Number. Bellard gives the exotic formula
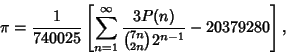 | (58) |
 | |  | (59) |
A complete listing of Ramanujan's  series for series for 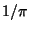 found in his second and third notebooks is given by Berndt (1994,pp. 352-354), found in his second and third notebooks is given by Berndt (1994,pp. 352-354), 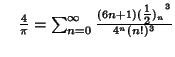 | (60) | 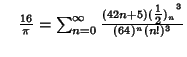 | (61) | 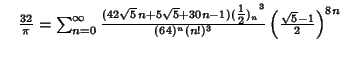 | (62) |  | (63) | 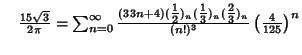 | (64) |  | (65) | 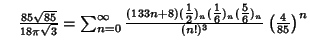 | (66) | 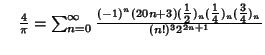 | (67) |
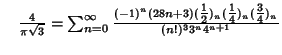 | (68) | 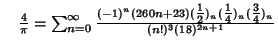 | (69) |  | (70) |  | (71) | 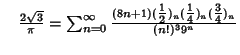 | (72) | 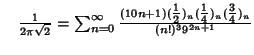 | (73) | 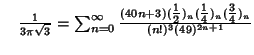 | (74) |  | (75) | 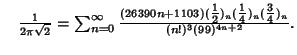 | (76) |
These equations were first proved by Borwein and Borwein (1987, pp. 177-187). Borwein and Borwein (1987b, 1988,1993) proved other equations of this type, and Chudnovsky and Chudnovsky (1987) found similar equations for othertranscendental constants.
A Spigot Algorithm for  is given by Rabinowitz and Wagon (1995). Amazingly, a closed form expression giving adigit extraction algorithm which produces digits of is given by Rabinowitz and Wagon (1995). Amazingly, a closed form expression giving adigit extraction algorithm which produces digits of  (or (or  ) in base-16 was recentlydiscovered by Bailey et al. (Bailey et al. 1995, Adamchik and Wagon 1997), ) in base-16 was recentlydiscovered by Bailey et al. (Bailey et al. 1995, Adamchik and Wagon 1997),
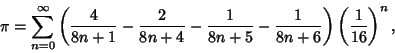 | (77) |
 | (78) |
 is given by the periodic sequence obtained by appending copies of is given by the periodic sequence obtained by appending copies of 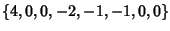 (inother words, (inother words, 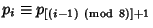 for for  ) and ) and 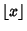 is the Floor Function. Thisexpression was discovered using the PSLQ Algorithm and is equivalent to is the Floor Function. Thisexpression was discovered using the PSLQ Algorithm and is equivalent to
 | (79) |
 | (80) |
 | (81) |
 th Digit of th Digit of  in any basein in any basein  steps. steps.
Another identity is
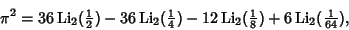 | (82) |
 is the Polylogarithm. (82) is equivalent to is the Polylogarithm. (82) is equivalent to
 | (83) |
 | (84) |
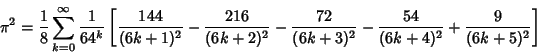 | (85) |
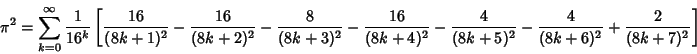 | (86) |
A slew of additional identities due to Ramanujan  , Catalan, and Newton , Catalan, and Newton  are given by Castellanos (1988,pp. 86-88), including several involving sums of Fibonacci Numbers. are given by Castellanos (1988,pp. 86-88), including several involving sums of Fibonacci Numbers.
Gasper quotes the result
 | (87) |
 is a Generalized Hypergeometric Function, and transforms it to is a Generalized Hypergeometric Function, and transforms it to
 | (88) |
 | (89) |
 | (90) |
 | | 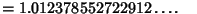 | (91) |
Another curious fact is the Almost Integer
 | (92) |
 | (93) |
 | (94) |
 | (95) |
 may also be computed using iterative Algorithms. A quadratically converging Algorithm due to Borwein is may also be computed using iterative Algorithms. A quadratically converging Algorithm due to Borwein is
and
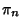 decreases monotonically to decreases monotonically to  with with
 | (102) |
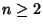 . The Brent-Salamin Formula is another quadratically converging algorithm which can be used tocalculate . The Brent-Salamin Formula is another quadratically converging algorithm which can be used tocalculate  . A quadratically convergent algorithm for . A quadratically convergent algorithm for  based on an observation by Salamin is given bydefining based on an observation by Salamin is given bydefining
 | (103) |
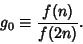 | (104) |
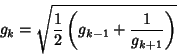 | (105) |
 | (106) |
A cubically converging Algorithm which converges to the nearest multiple of  to to 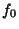 is the simple iteration is the simple iteration
 | (107) |
 | (108) |
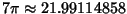 . .
A quartically converging Algorithm is obtained by letting
then defining
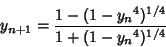 | (111) |
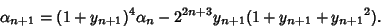 | (112) |
 | (113) |
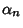 converges to converges to 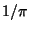 quartically with quartically with
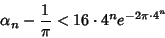 | (114) |
A quintically converging Algorithm is obtained by letting
Then let
 | (117) |
Finally, let
 | (121) |
 | (122) |
Another Algorithm is due to Woon (1995). Define  and and
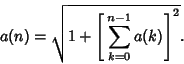 | (123) |
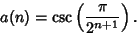 | (124) |
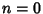 , the identity holds. If it holds for , the identity holds. If it holds for 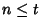 , then , then
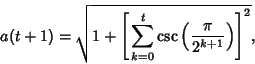 | (125) |
 | (126) |
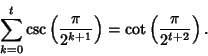 | (127) |
 | (128) |
 and, by induction, for all Nonnegative and, by induction, for all Nonnegative  , and , and
Other iterative Algorithms are the Archimedes Algorithm, which was derived by Pfaff in 1800, andthe Brent-Salamin Formula. Borwein et al. (1989) discuss  th order iterative algorithms. th order iterative algorithms.
Kochansky's Approximation is the Root of
 | (130) |
 | (131) |
 | (132) |
Some approximations due to Ramanujan 
 |  | 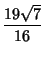 | (133) | | |  |  | (134) | | |  |  | (135) | | |  |  | (136) | | |  |  | (137) | | |  |  | (138) | | |  |  | (139) | | |  | 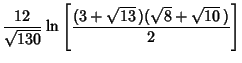 | (140) | | |  |  | (141) | | |  | 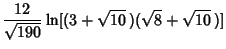 | (142) | | |  | 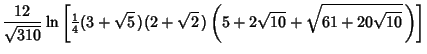 | (143) | | |  |  | (144) |
which are accurate to 3, 4, 4, 8, 8, 9, 14, 15, 15, 18, 23, 31 digits, respectively (Ramanujan  1913-1914; Hardy1952, p. 70; Berndt 1994, pp. 48-49 and 88-89). 1913-1914; Hardy1952, p. 70; Berndt 1994, pp. 48-49 and 88-89).
Castellanos (1988) gives a slew of curious formulas:
 |  | 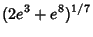 | (145) | | |  |  | (146) | | |  |  | (147) | | |  |  | (148) | | |  | 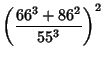 | (149) | | |  |  | | | | | | (150) | | |  | 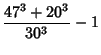 | (151) | | |  | 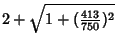 | (152) | | |  | 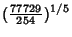 | (153) | | |  |  | (154) | | |  |  | (155) | | |  | 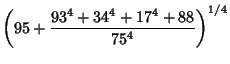 | (156) | | |  | 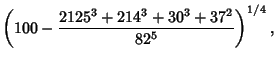 | (157) |
which are accurate to 3, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 12, and 13 digits, respectively. An extremely accurate approximationdue to Shanks (1982) is
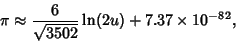 | (158) |
 is the product of four simple quartic units. A sequence of approximations due to Plouffe includes is the product of four simple quartic units. A sequence of approximations due to Plouffe includes
 |  |  | (159) | | |  |  | (160) | | |  |  | (161) | | |  | 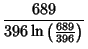 | (162) | | |  |  | (163) | | |  |  | (164) | | |  | 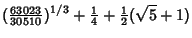 | (165) | | |  |  | (166) | | |  |  | (167) | | |  | 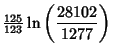 | (168) | | |  |  | (169) | | |  |  | (170) |
which are accurate to 4, 5, 7, 7, 8, 9, 10, 11, 11, 11, 23, and 30 digits, respectively.
Ramanujan  (1913-14) and Olds (1963) give geometric constructions for 355/113. Gardner (1966, pp. 92-93) givesa geometric construction for (1913-14) and Olds (1963) give geometric constructions for 355/113. Gardner (1966, pp. 92-93) givesa geometric construction for 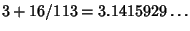 . Dixon (1991) gives constructions for . Dixon (1991) gives constructions for  and and  . Constructions for approximations of . Constructions for approximations of  are approximations toCircle Squaring (which is itself impossible). are approximations toCircle Squaring (which is itself impossible).
A short mnemonic for remembering the first eight Decimal Digits of  is ``May I have a largecontainer of coffee?'' giving 3.1415926 (Gardner 1959; Gardner 1966, p. 92; Eves 1990, p. 122, Davis 1993, p. 9). A moresubstantial mnemonic giving 15 digits (3.14159265358979) is ``How I want a drink, alcoholic of course, after the heavylectures involving quantum mechanics,'' originally due to Sir James Jeans (Gardner 1966, p. 92; Castellanos 1988, p. 152;Eves 1990, p. 122; Davis 1993, p. 9; Blatner 1997, p. 112). A slight extension of this adds the phrase ``All of thygeometry, Herr Planck, is fairly hard,'' giving 24 digits in all (3.14159265358979323846264). is ``May I have a largecontainer of coffee?'' giving 3.1415926 (Gardner 1959; Gardner 1966, p. 92; Eves 1990, p. 122, Davis 1993, p. 9). A moresubstantial mnemonic giving 15 digits (3.14159265358979) is ``How I want a drink, alcoholic of course, after the heavylectures involving quantum mechanics,'' originally due to Sir James Jeans (Gardner 1966, p. 92; Castellanos 1988, p. 152;Eves 1990, p. 122; Davis 1993, p. 9; Blatner 1997, p. 112). A slight extension of this adds the phrase ``All of thygeometry, Herr Planck, is fairly hard,'' giving 24 digits in all (3.14159265358979323846264).
An even more extensive rhyming mnemonic giving 31 digits is ``Now I will a rhyme construct, By chosen words the young instruct.Cunningly devised endeavour, Con it and remember ever. Widths in circle here you see, Sketched out in strange obscurity.'' (Notethat the British spelling of ``endeavour'' is required here.)
The following stanzas are the first part of a poem written by M. Keith based on Edgar Allen Poe's ``The Raven.'' The entirepoem gives 740 digits; the fragment below gives only the first 80 (Blatner 1997, p. 113). Words with ten letters represent thedigit 0, and those with 11 or more digits are taken to represent two digits.
Poe, E.: Near a Raven.
Midnights so dreary, tired and weary. Silently pondering volumes extolling all by-now obsolete lore. During my rather long nap-the weirdest tap! An ominous vibrating sound disturbing my chamber's antedoor. `This,' I whispered quietly, `I ignore.' Perfectly, the intellect remembers: the ghostly fires, a glittering ember.Inflamed by lightning's outbursts, windows cast penumbras upon this floor. Sorrowful, as one mistreated, unhappy thoughts I heeded:That inimitable lesson in elegance--Lenore-- Is delighting, exciting... nevermore.
An extensive collection of  mnemonics in many languages is maintained by A. P. Hatzipolakis. Other mnemonics invarious languages are given by Castellanos (1988) and Blatner (1997, pp. 112-118). mnemonics in many languages is maintained by A. P. Hatzipolakis. Other mnemonics invarious languages are given by Castellanos (1988) and Blatner (1997, pp. 112-118).
In the following, the word ``digit'' refers to decimal digit after the decimal point. J. H. Conway has shown thatthere is a sequence of fewer than 40 Fractions  , , 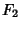 , ... with the property that if youstart with , ... with the property that if youstart with 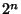 and repeatedly multiply by the first of the and repeatedly multiply by the first of the  that gives an integral answer, then the nextPower of 2 to occur will be the that gives an integral answer, then the nextPower of 2 to occur will be the 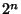 th decimal digit of th decimal digit of  . .
The first occurrence of  0s appear at digits 32, 307, 601, 13390, 17534, .... The sequence 9999998 occurs at decimal 762(which is sometimes called the Feynman Point). This is the largest value of any seven digits in the first milliondecimals. The first time the Beast Number 666 appears is decimal 2440. The digits 314159 appear at least six times inthe first 10 million decimal places of 0s appear at digits 32, 307, 601, 13390, 17534, .... The sequence 9999998 occurs at decimal 762(which is sometimes called the Feynman Point). This is the largest value of any seven digits in the first milliondecimals. The first time the Beast Number 666 appears is decimal 2440. The digits 314159 appear at least six times inthe first 10 million decimal places of  (Pickover 1995). In the following, ``digit'' means digit of (Pickover 1995). In the following, ``digit'' means digit of 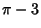 . The sequence0123456789 occurs beginning at digits 17,387,594,880, 26,852,899,245, 30,243,957,439, 34,549,153,953, 41,952,536,161, and43,289,964,000. The sequence 9876543210 occurs beginning at digits 21,981,157,633, 29,832,636,867, 39,232,573,648,42,140,457,481, and 43,065,796,214. The sequence 27182818284 (the digits of e) occur beginning at digit45,111,908,393. There are also interesting patterns for . The sequence0123456789 occurs beginning at digits 17,387,594,880, 26,852,899,245, 30,243,957,439, 34,549,153,953, 41,952,536,161, and43,289,964,000. The sequence 9876543210 occurs beginning at digits 21,981,157,633, 29,832,636,867, 39,232,573,648,42,140,457,481, and 43,065,796,214. The sequence 27182818284 (the digits of e) occur beginning at digit45,111,908,393. There are also interesting patterns for 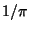 . 0123456789 occurs at 6,214,876,462, 9876543210 occurs at15,603,388,145 and 51,507,034,812, and 999999999999 occurs at 12,479,021,132 of . 0123456789 occurs at 6,214,876,462, 9876543210 occurs at15,603,388,145 and 51,507,034,812, and 999999999999 occurs at 12,479,021,132 of 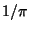 . .
Scanning the decimal expansion of  until all until all  -digit numbers have occurred, the last 1-, 2-, ... digit numbersappearing are 0, 68, 483, 6716, 33394, 569540, ... (Sloane's A032510). These end at digits 32, 606, 8555, 99849, 1369564,14118312, ... (Sloane's A036903). -digit numbers have occurred, the last 1-, 2-, ... digit numbersappearing are 0, 68, 483, 6716, 33394, 569540, ... (Sloane's A032510). These end at digits 32, 606, 8555, 99849, 1369564,14118312, ... (Sloane's A036903). See also Almost Integer, Archimedes Algorithm, Brent-Salamin Formula, Buffon-Laplace Needle Problem,Buffon's Needle Problem, Circle, Dirichlet Beta Function, Dirichlet Eta Function, DirichletLambda Function, e, Euler-Mascheroni Constant, Gaussian Distribution, Maclaurin Series,Machin's Formula, Machin-Like Formulas, Relatively Prime, Riemann Zeta Function, Sphere,Trigonometry
ReferencesAdamchik, V. and Wagon, S. ``A Simple Formula for  .'' Amer. Math. Monthly 104, 852-855, 1997. .'' Amer. Math. Monthly 104, 852-855, 1997.Almkvist, G. and Berndt, B. ``Gauss, Landen, Ramanujan, and Arithmetic-Geometric Mean, Ellipses,  , and the Ladies Diary.'' Amer. Math. Monthly 95, 585-608, 1988. , and the Ladies Diary.'' Amer. Math. Monthly 95, 585-608, 1988. Almkvist, G. ``Many Correct Digits of  , Revisited.'' Amer. Math. Monthly 104, 351-353, 1997. , Revisited.'' Amer. Math. Monthly 104, 351-353, 1997. Arndt, J. ``Cryptic Pi Related Formulas.'' http://www.jjj.de/hfloat/pise.dvi. Arndt, J. and Haenel, C. Pi: Algorithmen, Computer, Arithmetik. Berlin: Springer-Verlag, 1998. Assmus, E. F. ``Pi.'' Amer. Math. Monthly 92, 213-214, 1985. Bailey, D. H. ``Numerical Results on the Transcendence of Constants Involving  , ,  , and Euler's Constant.'' Math. Comput. 50, 275-281, 1988a. , and Euler's Constant.'' Math. Comput. 50, 275-281, 1988a. Bailey, D. H. ``The Computation of  to 29,360,000 Decimal Digit using Borwein's' Quartically Convergent Algorithm.'' Math. Comput. 50, 283-296, 1988b. to 29,360,000 Decimal Digit using Borwein's' Quartically Convergent Algorithm.'' Math. Comput. 50, 283-296, 1988b. Bailey, D.; Borwein, P.; and Plouffe, S. ``On the Rapid Computation of Various Polylogarithmic Constants.'' http://www.cecm.sfu.ca/~pborwein/PAPERS/P123.ps. Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 55 and 274, 1987. Beckmann, P. A History of Pi, 3rd ed. New York: Dorset Press, 1989. Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972. Berggren, L.; Borwein, J.; and Borwein, P. Pi: A Source Book. New York: Springer-Verlag, 1997. Bellard, F. ``Fabrice Bellard's Pi Page.'' http://www-stud.enst.fr/~bellard/pi/. Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994. Blatner, D. The Joy of Pi. New York: Walker, 1997. Blatner, D. ``The Joy of Pi.'' http://www.joyofpi.com. Borwein, P. B. ``Pi and Other Constants.'' http://www.cecm.sfu.ca/~pborwein/PISTUFF/Apistuff.html. Borwein, J. M. ``Ramanujan Type Series.'' http://www.cecm.sfu.ca/organics/papers/borwein/paper/html/local/omlink9/html/node1.html. Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987a. Borwein, J. M. and Borwein, P. B. ``Ramanujan's Rational and Algebraic Series for 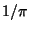 .'' Indian J. Math. 51, 147-160, 1987b. .'' Indian J. Math. 51, 147-160, 1987b. Borwein, J. M. and Borwein, P. B. ``More Ramanujan-Type Series for 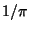 .'' In Ramanujan Revisited. Boston, MA: Academic Press, pp. 359-374, 1988. .'' In Ramanujan Revisited. Boston, MA: Academic Press, pp. 359-374, 1988. Borwein, J. M. and Borwein, P. B. ``Class Number Three Ramanujan Type Series for 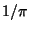 .'' J. Comput. Appl. Math. 46, 281-290, 1993. .'' J. Comput. Appl. Math. 46, 281-290, 1993. Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. ``Ramanujan, Modular Equations, and Approximations to Pi, or How to Compute One Billion Digits of Pi.'' Amer. Math. Monthly 96, 201-219, 1989. Brown, K. S. ``Rounding Up to Pi.'' http://www.seanet.com/~ksbrown/kmath001.htm. Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988. Castellanos, D. ``The Ubiquitous Pi. Part II.'' Math. Mag. 61, 148-163, 1988. Chan, J. ``As Easy as Pi.'' Math Horizons, Winter 1993, pp. 18-19, 1993. Chudnovsky, D. V. and Chudnovsky, G. V. Padé and Rational Approximations to Systems of Functions and Their Arithmetic Applications. Berlin: Springer-Verlag, 1984. Chudnovsky, D. V. and Chudnovsky, G. V. ``Approximations and Complex Multiplication According to Ramanujan.'' In Ramanujan Revisited: Proceedings of the Centenary Conference (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). Boston, MA: Academic Press, pp. 375-472, 1987. Conway, J. H. and Guy, R. K. ``The Number  .'' In The Book of Numbers. New York: Springer-Verlag, pp. 237-239, 1996. .'' In The Book of Numbers. New York: Springer-Verlag, pp. 237-239, 1996. David, Y. ``On a Sequence Generated by a Sieving Process.'' Riveon Lematematika 11, 26-31, 1957. Davis, D. M. The Nature and Power of Mathematics. Princeton, NJ: Princeton University Press, 1993. Dixon, R. ``The Story of Pi ( ).'' §4.3 in Mathographics. New York: Dover, pp. 44-49 and 98-101, 1991. ).'' §4.3 in Mathographics. New York: Dover, pp. 44-49 and 98-101, 1991. Dunham, W. ``A Gem from Isaac Newton.'' Ch. 7 in Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 106-112 and 155-183, 1990. Eves, H. An Introduction to the History of Mathematics, 6th ed. Philadelphia, PA: Saunders, 1990. Exploratorium. `` Page.'' http://www.exploratorium.edu/learning_studio/pi/. Page.'' http://www.exploratorium.edu/learning_studio/pi/. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/pi/pi.html Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript. 1996. http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps. Gardner, M. ``Memorizing Numbers.'' Ch. 11 in The Scientific American Book of Mathematical Puzzles and Diversions. New York: Simon and Schuster, p. 103, 1959. Gardner, M. ``The Transcendental Number Pi.'' Ch. 8 in Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, 1966. Gosper, R. W. Table of Simple Continued Fraction for  and the Derived Decimal Approximation. Stanford, CA: Artificial Intelligence Laboratory, Stanford University, Oct. 1975. Reviewed in Math. Comput. 31, 1044, 1977. and the Derived Decimal Approximation. Stanford, CA: Artificial Intelligence Laboratory, Stanford University, Oct. 1975. Reviewed in Math. Comput. 31, 1044, 1977. Hardy, G. H. A Course of Pure Mathematics, 10th ed. Cambridge, England: Cambridge University Press, 1952. Hatzipolakis, A. P. ``PiPhilology.'' http://users.hol.gr/~xpolakis/piphil.html. Hobsen, E. W. Squaring the Circle. New York: Chelsea, 1988. Johnson-Hill, N. ``Extraordinary Pi.'' http://www.users.globalnet.co.uk/~nickjh/Pi.htm. Johnson-Hill, N. ``The Biggest Selection of Pi Links on the Internet.'' http://www.users.globalnet.co.uk/~nickjh/pi_links.htm. Kanada, Y. ``New World Record of Pi: 51.5 Billion Decimal Digits.'' http://www.cecm.sfu.ca/personal/jborwein/Kanada_50b.html. Klein, F. Famous Problems. New York: Chelsea, 1955. Knopp, K. §32, 136, and 138 in Theory and Application of Infinite Series. New York: Dover, p. 238, 1990. Laczkovich, M. ``On Lambert's Proof of the Irrationality of  .'' Amer. Math. Monthly 104, 439-443, 1997. .'' Amer. Math. Monthly 104, 439-443, 1997. Lambert, J. H. ``Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques.'' Mémoires de l'Academie des sciences de Berlin 17, 265-322, 1761. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 22 and 50, 1983. Lindemann, F. ``Über die Zahl  .'' Math. Ann. 20, 213-225, 1882. .'' Math. Ann. 20, 213-225, 1882. Lopez, A. ``Indiana Bill Sets the Value of  to 3.'' http://daisy.uwaterloo.ca/~alopez-o/math-faq/mathtext/node19.html. to 3.'' http://daisy.uwaterloo.ca/~alopez-o/math-faq/mathtext/node19.html. MacTutor Archive. ``Pi Through the Ages.'' http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Pi_through_the_ages.html. Mahler, K. ``On the Approximation of  .'' Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953. .'' Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953. Ogilvy, C. S. ``Pi and Pi-Makers.'' Ch. 10 in Excursions in Mathematics. New York: Dover, pp. 108-120, 1994. Olds, C. D. Continued Fractions. New York: Random House, pp. 59-60, 1963. Pappas, T. ``Probability and  .'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 18-19, 1989. .'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 18-19, 1989. Peterson, I. Islands of Truth: A Mathematical Mystery Cruise. New York: W. H. Freeman, pp. 178-186, 1990. Pickover, C. A. Keys to Infinity. New York: Wiley, p. 62, 1995. Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computationof Constants.'' http://www.lacim.uqam.ca/pi/records.html. Plouffe, S. ``People Who Computed Pi.'' http://www.cecm.sfu.ca/projects/ISC/records.html. Plouffe, S. ``Plouffe's Inverter: A Few Approximations of Pi.'' http://www.lacim.uqam.ca/pi/approxpi.html. Plouffe, S. ``The  Page.'' http://www.cecm.sfu.ca/pi/. Page.'' http://www.cecm.sfu.ca/pi/. Plouffe, S. ``Table of Computation of Pi from 2000 BC to Now.'' http://www.cecm.sfu.ca/projects/ISC/Pihistory.html. Preston, R. ``Mountains of Pi.'' New Yorker 68, 36-67, Mar. 2, 1992. http://www.lacim.uqam.ca/plouffe/Chudnovsky.html. Project Mathematics! The Story of Pi. Videotape (24 minutes). California Institute of Technology. Available from the Math. Assoc. Amer. Rabinowitz, S. and Wagon, S. ``A Spigot Algorithm for the Digits of  .'' Amer. Math. Monthly 102, 195-203, 1995. .'' Amer. Math. Monthly 102, 195-203, 1995. Ramanujan, S. ``Modular Equations and Approximations to  .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914. .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914. Rudio, F. ``Archimedes, Huygens, Lambert, Legendre.'' In Vier Abhandlungen über die Kreismessung. Leipzig, Germany, 1892. Shanks, D. ``Dihedral Quartic Approximations and Series for  .'' J. Number. Th. 14, 397-423, 1982. .'' J. Number. Th. 14, 397-423, 1982. Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993. Singh, S. Fermat's Enigma: The Epic Quest to Solve the World's Greatest Mathematical Problem. New York: Walker, pp. 17-18, 1997. Sloane, N. J. A. Sequences A000796/M2218, A001203/M2646, A001901/M, A002485/M3097, A002486/M4456, A002491/M1009, A007509/M2061, A025547, A032510, A032523 A033089, A033090, A036903, and A046126 in in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Stéllum, H.-H. ``River Meandering as a Self-Organization Process.'' Science 271, 1710-1713, 1996. Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991. Viète, F. Uriorum de rebus mathematicis responsorum, liber VIII, 1593. Wagon, S. ``Is  Normal?'' Math. Intel. 7, 65-67, 1985. Normal?'' Math. Intel. 7, 65-67, 1985. Whitcomb, C. ``Notes on Pi ( ).'' http://witcombe.sbc.edu/EMPi.html. ).'' http://witcombe.sbc.edu/EMPi.html. Woon, S. C. ``Problem 1441.'' Math. Mag. 68, 72-73, 1995. |

![]() which is defined as the ratio of a Circle's Circumference
which is defined as the ratio of a Circle's Circumference ![]() to itsDiameter
to itsDiameter ![]() ,
,![]() , which gives the ``best'' approximation of a given order, is [3, 7, 15, 1, 292, 1, 1,1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, ...] (Sloane's A001203). The very large term 292 means that the Convergent
, which gives the ``best'' approximation of a given order, is [3, 7, 15, 1, 292, 1, 1,1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, ...] (Sloane's A001203). The very large term 292 means that the Convergent![]() 's Continued Fraction (Gosper 1977, Ball and Coxeter 1987), although thecomputer on which the numbers are stored may no longer be functional (Gosper, pers. comm., 1998). According to Gosper, atypical Continued Fraction term carries only slightly more significance than a decimal Digit. The sequence ofincreasing terms in the A033089), occurring at positions1, 2, 3, 5, 308, 432, ... (Sloane's A033090). In the first 26,491 terms of the Continued Fraction (counting 3 as the0th), the only five-Digit terms are 20,776 (the 431st), 19,055 (15,543rd), and 19,308 (23,398th) (Beeler et al. 1972,Item 140). The first 6-Digit term is 528,210 (the 267,314th), and the first 8-Digit term is 12,996,958(453,294th). The term having the largest known value is the whopping 9-Digit 87,878,3625 (the 11,504,931st term).
's Continued Fraction (Gosper 1977, Ball and Coxeter 1987), although thecomputer on which the numbers are stored may no longer be functional (Gosper, pers. comm., 1998). According to Gosper, atypical Continued Fraction term carries only slightly more significance than a decimal Digit. The sequence ofincreasing terms in the A033089), occurring at positions1, 2, 3, 5, 308, 432, ... (Sloane's A033090). In the first 26,491 terms of the Continued Fraction (counting 3 as the0th), the only five-Digit terms are 20,776 (the 431st), 19,055 (15,543rd), and 19,308 (23,398th) (Beeler et al. 1972,Item 140). The first 6-Digit term is 528,210 (the 267,314th), and the first 8-Digit term is 12,996,958(453,294th). The term having the largest known value is the whopping 9-Digit 87,878,3625 (the 11,504,931st term).![]() does not show any obvious patterns, but clear patterns do emerge in thebeautiful non-simple Continued Fractions
does not show any obvious patterns, but clear patterns do emerge in thebeautiful non-simple Continued Fractions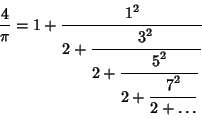
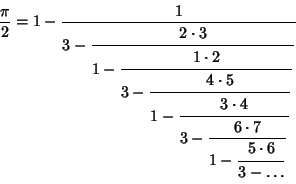
![]() crops up in all sorts of unexpected places in mathematics besides Circles and Spheres. For example, it occurs in the normalization of the Gaussian Distribution, in the distribution of Primes,in the construction of numbers which are very close to Integers (the Ramanujan Constant),and in the probability that a pin dropped on a set of Parallel lines intersects a line (Buffon's NeedleProblem). Pi also appears as the average ratio of the actual length and the direct distance between source and mouth in ameandering river (Stéllum 1996, Singh 1997).
crops up in all sorts of unexpected places in mathematics besides Circles and Spheres. For example, it occurs in the normalization of the Gaussian Distribution, in the distribution of Primes,in the construction of numbers which are very close to Integers (the Ramanujan Constant),and in the probability that a pin dropped on a set of Parallel lines intersects a line (Buffon's NeedleProblem). Pi also appears as the average ratio of the actual length and the direct distance between source and mouth in ameandering river (Stéllum 1996, Singh 1997).![]() is sometimes known as Ludolph's Constantafter Ludolph van Ceulen (1539-1610), a Dutch
is sometimes known as Ludolph's Constantafter Ludolph van Ceulen (1539-1610), a Dutch ![]() calculator. The symbol
calculator. The symbol ![]() was first used by William Jones in 1706, andsubsequently adopted by Euler.
was first used by William Jones in 1706, andsubsequently adopted by Euler. ![]() In Measurement of a Circle, Archimedes
In Measurement of a Circle, Archimedes ![]() (ca. 225BC
(ca. 225BC ![]() ) obtained the first rigorous approximation by Inscribing andCircumscribing
) obtained the first rigorous approximation by Inscribing andCircumscribing ![]() -gons on a Circle using the Archimedes Algorithm. Using
-gons on a Circle using the Archimedes Algorithm. Using ![]() (a 96-gon), Archimedes
(a 96-gon), Archimedes ![]() obtained
obtained![]() . It should bementioned, however, that both instances refer to a value obtained from physical measurements and, as such, are probablywell within the bounds of experimental uncertainty. I Kings 7:23 states, ``Also he made a molten sea of tenCubits
. It should bementioned, however, that both instances refer to a value obtained from physical measurements and, as such, are probablywell within the bounds of experimental uncertainty. I Kings 7:23 states, ``Also he made a molten sea of tenCubits ![]() from brim to brim, round in compass, and five cubits in height thereof; and a line thirtycubits did compass it round about.'' This implies
from brim to brim, round in compass, and five cubits in height thereof; and a line thirtycubits did compass it round about.'' This implies ![]() . The Babylonians gave an estimate of
. The Babylonians gave an estimate of ![]() as
as ![]() . The Egyptians did better still, obtaining
. The Egyptians did better still, obtaining ![]() in the Rhind papyrus, and 22/7 elsewhere. TheChinese geometers, however, did best of all, rigorously deriving
in the Rhind papyrus, and 22/7 elsewhere. TheChinese geometers, however, did best of all, rigorously deriving ![]() to 6 decimal places.
to 6 decimal places.![]() can be used to estimate
can be used to estimate ![]() by starting with an
by starting with an ![]() -gon and thenrelating the Area of subsequent
-gon and thenrelating the Area of subsequent ![]() -gons. Let
-gons. Let ![]() be the Angle from the center of one of thePolygon's segments,
be the Angle from the center of one of thePolygon's segments,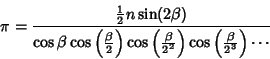
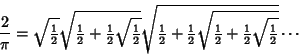
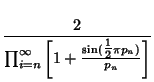



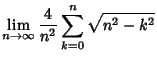
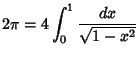

![]() is known to be Irrational (Lambert 1761, Legendre 1794) and evenTranscendental (Lindemann 1882). Incidentally, Lindemann's proof of the transcendence of
is known to be Irrational (Lambert 1761, Legendre 1794) and evenTranscendental (Lindemann 1882). Incidentally, Lindemann's proof of the transcendence of![]() also proved that the Geometric Problem of Antiquity known as CircleSquaring is impossible. A simplified, but still difficult, version of Lindemann's proof is given by Klein (1955).
also proved that the Geometric Problem of Antiquity known as CircleSquaring is impossible. A simplified, but still difficult, version of Lindemann's proof is given by Klein (1955).![]() is not a Liouville Number (Mahler 1953). In 1974, M. Mignotte showed that
is not a Liouville Number (Mahler 1953). In 1974, M. Mignotte showed that![]() are also very uniformly distributed (
are also very uniformly distributed (![]() ), as shown in the following table.
), as shown in the following table.![]() ,
, ![]() , or
, or ![]() are Irrational. However, it is known that theycannot satisfy any Polynomial equation of degree
are Irrational. However, it is known that theycannot satisfy any Polynomial equation of degree ![]() with Integer Coefficients ofaverage size 10
with Integer Coefficients ofaverage size 10![]() satisfies the Inequality
satisfies the Inequality![]()
![]() , round up to the nearest multiple of
, round up to the nearest multiple of ![]() , then up to the nearest multipleof
, then up to the nearest multipleof ![]() , and so on, up to the nearest multiple of 1. Let
, and so on, up to the nearest multiple of 1. Let ![]() denote the result. Then the ratio
denote the result. Then the ratio![]()
![]()
![]() are 1, 2, 4, 6, 10, 12, 18, 22, 30, 34, ... (Sloane's A002491).
are 1, 2, 4, 6, 10, 12, 18, 22, 30, 34, ... (Sloane's A002491).
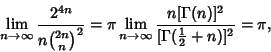
![]() denotes a Binomial Coefficient and
denotes a Binomial Coefficient and ![]() is the Gamma Function (Knopp 1990).Euler
is the Gamma Function (Knopp 1990).Euler ![]() obtained
obtained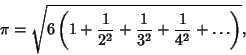
![]() . SimilarFormulas follow from
. SimilarFormulas follow from ![]() for all Positive Integers
for all Positive Integers ![]() . Gregory
. Gregory ![]() and Leibniz
and Leibniz ![]() found
found![]()
![]() th term of this series in Gregory's Formulais larger than
th term of this series in Gregory's Formulais larger than ![]() so this sum converges so slowly that 300 terms are not sufficient to calculate
so this sum converges so slowly that 300 terms are not sufficient to calculate ![]() correctly totwo decimal places! However, it can be transformed to
correctly totwo decimal places! However, it can be transformed to
![]() is the Riemann Zeta Function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the errorafter
is the Riemann Zeta Function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the errorafter ![]() terms is
terms is ![]() . Newton
. Newton ![]() used
used![]()
![]()
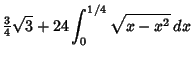
![]()
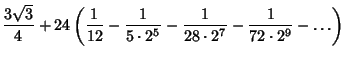
![]() Convergence Improvement transformation gives
Convergence Improvement transformation gives![]()
![]()
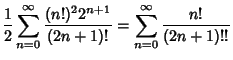
![]()
![]()
![]()
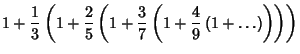
![]() into the Power Series for theHypergeometric Function
into the Power Series for theHypergeometric Function ![]() ,
,
![]() gives 2 bits/term,
gives 2 bits/term,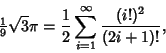
![]() gives almost 3.39 bits/term,
gives almost 3.39 bits/term,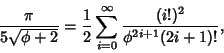
![]() is the Golden Ratio. Gosper also obtained
is the Golden Ratio. Gosper also obtained![]()
![]() is
is
![]() (1913-14),
(1913-14),![]()
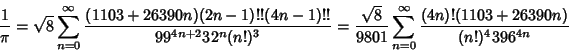
![]()
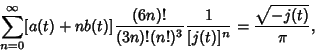
![]() is a Quadratic Form Discriminant,
is a Quadratic Form Discriminant, ![]() is the j-Function,
is the j-Function,![]()
![]()
![]()
![]()
![]()

![]() are Ramanujan-Eisenstein Series. A Class Number
are Ramanujan-Eisenstein Series. A Class Number ![]() field involves
field involves ![]() th degree AlgebraicIntegers of the constants
th degree AlgebraicIntegers of the constants ![]() ,
, ![]() , and
, and ![]() . The fastest converging series that uses onlyInteger terms corresponds to the largest Class Number 1 discriminant of
. The fastest converging series that uses onlyInteger terms corresponds to the largest Class Number 1 discriminant of ![]() and was formulated by theChudnovsky brothers (1987). The 163 appearing here is the same one appearing in the fact that
and was formulated by theChudnovsky brothers (1987). The 163 appearing here is the same one appearing in the fact that ![]() (theRamanujan Constant) is very nearly an Integer. The series is given by
(theRamanujan Constant) is very nearly an Integer. The series is given by![]()
![]()

![]()
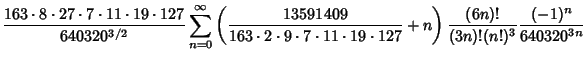
![]() (Wolfram Research,Champaign, IL) to calculate
(Wolfram Research,Champaign, IL) to calculate ![]() (Vardi 1991),
(Vardi 1991),![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ) is
) is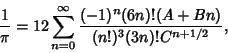
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and gives 37-38 digits per term. The fastest converging ClassNumber 4 series corresponds to
and gives 37-38 digits per term. The fastest converging ClassNumber 4 series corresponds to ![]() and is
and is
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
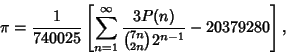
![]()
![]()
![]() series for
series for ![]() found in his second and third notebooks is given by Berndt (1994,pp. 352-354),
found in his second and third notebooks is given by Berndt (1994,pp. 352-354),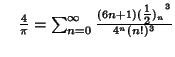
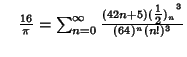
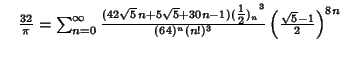

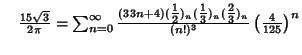

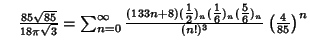
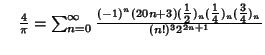
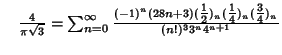
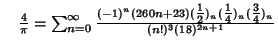


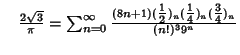
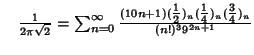
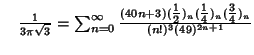

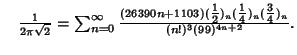
![]() is given by Rabinowitz and Wagon (1995). Amazingly, a closed form expression giving adigit extraction algorithm which produces digits of
is given by Rabinowitz and Wagon (1995). Amazingly, a closed form expression giving adigit extraction algorithm which produces digits of ![]() (or
(or ![]() ) in base-16 was recentlydiscovered by Bailey et al. (Bailey et al. 1995, Adamchik and Wagon 1997),
) in base-16 was recentlydiscovered by Bailey et al. (Bailey et al. 1995, Adamchik and Wagon 1997),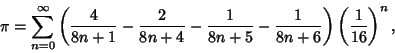

![]() is given by the periodic sequence obtained by appending copies of
is given by the periodic sequence obtained by appending copies of ![]() (inother words,
(inother words, ![]() for
for ![]() ) and
) and ![]() is the Floor Function. Thisexpression was discovered using the PSLQ Algorithm and is equivalent to
is the Floor Function. Thisexpression was discovered using the PSLQ Algorithm and is equivalent to![]()
![]()

![]() th Digit of
th Digit of ![]() in any basein
in any basein ![]() steps.
steps.![]()
![]() is the Polylogarithm. (82) is equivalent to
is the Polylogarithm. (82) is equivalent to
![]()
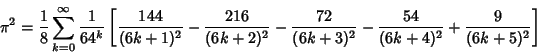
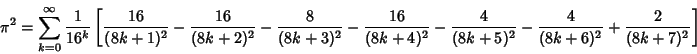
![]() , Catalan, and Newton
, Catalan, and Newton ![]() are given by Castellanos (1988,pp. 86-88), including several involving sums of Fibonacci Numbers.
are given by Castellanos (1988,pp. 86-88), including several involving sums of Fibonacci Numbers.![]()
![]() is a Generalized Hypergeometric Function, and transforms it to
is a Generalized Hypergeometric Function, and transforms it to![]()



![]()
![]()
![]()
![]()
![]()
![]() may also be computed using iterative Algorithms. A quadratically converging Algorithm due to Borwein is
may also be computed using iterative Algorithms. A quadratically converging Algorithm due to Borwein is![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()

![]()
![]()
![]()
![]() decreases monotonically to
decreases monotonically to ![]() with
with![]()
![]() . The Brent-Salamin Formula is another quadratically converging algorithm which can be used tocalculate
. The Brent-Salamin Formula is another quadratically converging algorithm which can be used tocalculate ![]() . A quadratically convergent algorithm for
. A quadratically convergent algorithm for ![]() based on an observation by Salamin is given bydefining
based on an observation by Salamin is given bydefining
![]()
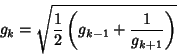

![]() to
to ![]() is the simple iteration
is the simple iteration![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() converges to
converges to ![]() quartically with
quartically with![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and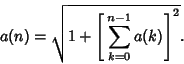
![]()
![]() , the identity holds. If it holds for
, the identity holds. If it holds for ![]() , then
, then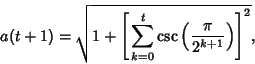
![]()
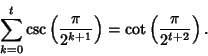
![]()
![]() and, by induction, for all Nonnegative
and, by induction, for all Nonnegative ![]() , and
, and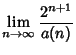
![]()
![]()
![]()

![]()

![]() th order iterative algorithms.
th order iterative algorithms.![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()

![]()
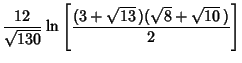
![]()

![]()
![]()
![]()
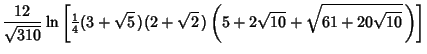
![]()

![]() 1913-1914; Hardy1952, p. 70; Berndt 1994, pp. 48-49 and 88-89).
1913-1914; Hardy1952, p. 70; Berndt 1994, pp. 48-49 and 88-89).![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
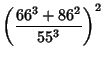
![]()
![]()
![]()
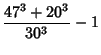
![]()
![]()
![]()
![]()
![]()

![]()

![]()
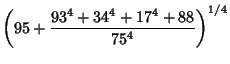
![]()
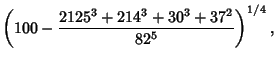
![]()
![]() is the product of four simple quartic units. A sequence of approximations due to Plouffe includes
is the product of four simple quartic units. A sequence of approximations due to Plouffe includes![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()
![]()
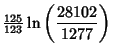
![]()
![]()
![]()

![]() (1913-14) and Olds (1963) give geometric constructions for 355/113. Gardner (1966, pp. 92-93) givesa geometric construction for
(1913-14) and Olds (1963) give geometric constructions for 355/113. Gardner (1966, pp. 92-93) givesa geometric construction for ![]() . Dixon (1991) gives constructions for
. Dixon (1991) gives constructions for ![]() and
and ![]() . Constructions for approximations of
. Constructions for approximations of ![]() are approximations toCircle Squaring (which is itself impossible).
are approximations toCircle Squaring (which is itself impossible).![]() is ``May I have a largecontainer of coffee?'' giving 3.1415926 (Gardner 1959; Gardner 1966, p. 92; Eves 1990, p. 122, Davis 1993, p. 9). A moresubstantial mnemonic giving 15 digits (3.14159265358979) is ``How I want a drink, alcoholic of course, after the heavylectures involving quantum mechanics,'' originally due to Sir James Jeans (Gardner 1966, p. 92; Castellanos 1988, p. 152;Eves 1990, p. 122; Davis 1993, p. 9; Blatner 1997, p. 112). A slight extension of this adds the phrase ``All of thygeometry, Herr Planck, is fairly hard,'' giving 24 digits in all (3.14159265358979323846264).
is ``May I have a largecontainer of coffee?'' giving 3.1415926 (Gardner 1959; Gardner 1966, p. 92; Eves 1990, p. 122, Davis 1993, p. 9). A moresubstantial mnemonic giving 15 digits (3.14159265358979) is ``How I want a drink, alcoholic of course, after the heavylectures involving quantum mechanics,'' originally due to Sir James Jeans (Gardner 1966, p. 92; Castellanos 1988, p. 152;Eves 1990, p. 122; Davis 1993, p. 9; Blatner 1997, p. 112). A slight extension of this adds the phrase ``All of thygeometry, Herr Planck, is fairly hard,'' giving 24 digits in all (3.14159265358979323846264). ![]() mnemonics in many languages is maintained by A. P. Hatzipolakis. Other mnemonics invarious languages are given by Castellanos (1988) and Blatner (1997, pp. 112-118).
mnemonics in many languages is maintained by A. P. Hatzipolakis. Other mnemonics invarious languages are given by Castellanos (1988) and Blatner (1997, pp. 112-118).![]() ,
, ![]() , ... with the property that if youstart with
, ... with the property that if youstart with ![]() and repeatedly multiply by the first of the
and repeatedly multiply by the first of the ![]() that gives an integral answer, then the nextPower of 2 to occur will be the
that gives an integral answer, then the nextPower of 2 to occur will be the ![]() th decimal digit of
th decimal digit of ![]() .
.![]() 0s appear at digits 32, 307, 601, 13390, 17534, .... The sequence 9999998 occurs at decimal 762(which is sometimes called the Feynman Point). This is the largest value of any seven digits in the first milliondecimals. The first time the Beast Number 666 appears is decimal 2440. The digits 314159 appear at least six times inthe first 10 million decimal places of
0s appear at digits 32, 307, 601, 13390, 17534, .... The sequence 9999998 occurs at decimal 762(which is sometimes called the Feynman Point). This is the largest value of any seven digits in the first milliondecimals. The first time the Beast Number 666 appears is decimal 2440. The digits 314159 appear at least six times inthe first 10 million decimal places of ![]() (Pickover 1995). In the following, ``digit'' means digit of
(Pickover 1995). In the following, ``digit'' means digit of ![]() . The sequence0123456789 occurs beginning at digits 17,387,594,880, 26,852,899,245, 30,243,957,439, 34,549,153,953, 41,952,536,161, and43,289,964,000. The sequence 9876543210 occurs beginning at digits 21,981,157,633, 29,832,636,867, 39,232,573,648,42,140,457,481, and 43,065,796,214. The sequence 27182818284 (the digits of e) occur beginning at digit45,111,908,393. There are also interesting patterns for
. The sequence0123456789 occurs beginning at digits 17,387,594,880, 26,852,899,245, 30,243,957,439, 34,549,153,953, 41,952,536,161, and43,289,964,000. The sequence 9876543210 occurs beginning at digits 21,981,157,633, 29,832,636,867, 39,232,573,648,42,140,457,481, and 43,065,796,214. The sequence 27182818284 (the digits of e) occur beginning at digit45,111,908,393. There are also interesting patterns for ![]() . 0123456789 occurs at 6,214,876,462, 9876543210 occurs at15,603,388,145 and 51,507,034,812, and 999999999999 occurs at 12,479,021,132 of
. 0123456789 occurs at 6,214,876,462, 9876543210 occurs at15,603,388,145 and 51,507,034,812, and 999999999999 occurs at 12,479,021,132 of ![]() .
.![]() until all
until all ![]() -digit numbers have occurred, the last 1-, 2-, ... digit numbersappearing are 0, 68, 483, 6716, 33394, 569540, ... (Sloane's A032510). These end at digits 32, 606, 8555, 99849, 1369564,14118312, ... (Sloane's A036903).
-digit numbers have occurred, the last 1-, 2-, ... digit numbersappearing are 0, 68, 483, 6716, 33394, 569540, ... (Sloane's A032510). These end at digits 32, 606, 8555, 99849, 1369564,14118312, ... (Sloane's A036903).![]() .'' Amer. Math. Monthly 104, 852-855, 1997.
.'' Amer. Math. Monthly 104, 852-855, 1997.![]() , and the Ladies Diary.'' Amer. Math. Monthly 95, 585-608, 1988.
, and the Ladies Diary.'' Amer. Math. Monthly 95, 585-608, 1988.![]() , Revisited.'' Amer. Math. Monthly 104, 351-353, 1997.
, Revisited.'' Amer. Math. Monthly 104, 351-353, 1997.![]() ,
, ![]() , and Euler's Constant.'' Math. Comput. 50, 275-281, 1988a.
, and Euler's Constant.'' Math. Comput. 50, 275-281, 1988a.![]() to 29,360,000 Decimal Digit using Borwein's' Quartically Convergent Algorithm.'' Math. Comput. 50, 283-296, 1988b.
to 29,360,000 Decimal Digit using Borwein's' Quartically Convergent Algorithm.'' Math. Comput. 50, 283-296, 1988b.![]() .'' Indian J. Math. 51, 147-160, 1987b.
.'' Indian J. Math. 51, 147-160, 1987b.![]() .'' In Ramanujan Revisited. Boston, MA: Academic Press, pp. 359-374, 1988.
.'' In Ramanujan Revisited. Boston, MA: Academic Press, pp. 359-374, 1988.![]() .'' J. Comput. Appl. Math. 46, 281-290, 1993.
.'' J. Comput. Appl. Math. 46, 281-290, 1993.![]() .'' In The Book of Numbers. New York: Springer-Verlag, pp. 237-239, 1996.
.'' In The Book of Numbers. New York: Springer-Verlag, pp. 237-239, 1996.![]() ).'' §4.3 in Mathographics. New York: Dover, pp. 44-49 and 98-101, 1991.
).'' §4.3 in Mathographics. New York: Dover, pp. 44-49 and 98-101, 1991.![]() Page.'' http://www.exploratorium.edu/learning_studio/pi/.
Page.'' http://www.exploratorium.edu/learning_studio/pi/.![]() and the Derived Decimal Approximation. Stanford, CA: Artificial Intelligence Laboratory, Stanford University, Oct. 1975. Reviewed in Math. Comput. 31, 1044, 1977.
and the Derived Decimal Approximation. Stanford, CA: Artificial Intelligence Laboratory, Stanford University, Oct. 1975. Reviewed in Math. Comput. 31, 1044, 1977.![]() .'' Amer. Math. Monthly 104, 439-443, 1997.
.'' Amer. Math. Monthly 104, 439-443, 1997.![]() .'' Math. Ann. 20, 213-225, 1882.
.'' Math. Ann. 20, 213-225, 1882.![]() to 3.'' http://daisy.uwaterloo.ca/~alopez-o/math-faq/mathtext/node19.html.
to 3.'' http://daisy.uwaterloo.ca/~alopez-o/math-faq/mathtext/node19.html.![]() .'' Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953.
.'' Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953.![]() .'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 18-19, 1989.
.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 18-19, 1989.![]() Page.'' http://www.cecm.sfu.ca/pi/.
Page.'' http://www.cecm.sfu.ca/pi/.![]() .'' Amer. Math. Monthly 102, 195-203, 1995.
.'' Amer. Math. Monthly 102, 195-203, 1995.![]() .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.![]() .'' J. Number. Th. 14, 397-423, 1982.
.'' J. Number. Th. 14, 397-423, 1982.![]() Normal?'' Math. Intel. 7, 65-67, 1985.
Normal?'' Math. Intel. 7, 65-67, 1985.![]() ).'' http://witcombe.sbc.edu/EMPi.html.
).'' http://witcombe.sbc.edu/EMPi.html.