请输入您要查询的字词：

　

单词 Smarandache Sequences
释义

Smarandache Sequences

Smarandache sequences are any of a number of simply generated Integer Sequences resembling thoseconsidered in published works by Smarandache such as the Consecutive Number Sequences and EuclidNumbers (Iacobescu 1997). Other Smarandache-type sequences are given below.

1. The concatenation of 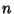copies of the Integer 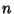: 1, 22, 333, 4444, 55555, ... (Sloane's A000461; Marimutha 1997),

2. The concatenation of the first 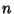Fibonacci Numbers: 1, 11, 112, 1123, 11235, ... (Sloane's A019523; Marimutha 1997),

3. The smallest number that is the sum of squares of two distinct earlier terms: 1, 2, 5, 26, 29, 677, ... (Sloane's A008318, Bencze 1997),

4. The smallest number that is the sum of squares of any number of distinct earlier terms: 1, 1, 2, 4, 5, 6, 16, 17, ... (Sloane's A008319, Bencze 1997),

5. The smallest number that is not the sum of squares of two distinct earlier terms: 1, 2, 3, 4, 6, 7, 8, 9, 11, ... (Sloane's A008320, Bencze 1997),

6. The smallest number that is not the sum of squares of any number of distinct earlier terms: 1, 2, 3, 6, 7, 8, 11, ... (Sloane's A008321, Bencze 1997),

7. The smallest number that is a sum of cubes of two distinct earlier terms: 1, 2, 9, 730, 737, ... (Sloane's A008322, Bencze 1997),

8. The smallest number that is a sum of cubes of any number of distinct earlier terms: 1, 1, 2, 8, 9, 10, 512, 513, 514, ... (Sloane's A019511, Bencze 1997),

9. The smallest number that is not a sum of cubes of two distinct earlier terms: 1, 2, 3, 4, 5, 6, 7, 8, 10, ... (Sloane's A031980, Bencze 1997),

10. The smallest number that is not a sum of cubes of any number of distinct earlier terms: 1, 2, 3, 4, 5, 6, 7, 10, 11, ... (Sloane's A031981, Bencze 1997),

11. The number of Partitions of a number , 2, ... into Square Numbers: 1, 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, 4, 5, 6, 6, 6, 8, 9, 10, 10, 12, 13, ... (Sloane's A001156, Iacobescu 1997),

12. The number of Partitions of a number , 2, ... into Cubic Numbers:1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, ... (Sloane's A003108, Iacobescu 1997),

13. Two copies of the first 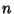Positive integers: 11, 1212, 123123, 12341234, ... (Sloane's A019524, Iacobescu 1997),

14. Numbers written in base of triangular numbers: 1, 2, 10, 11, 12, 100, 101, 102, 110, 1000, 1001, 1002, ... (Sloane's A000462, Iacobescu 1997),

15. Numbers written in base of double factorial numbers: 1, 10, 100, 101, 110, 200, 201, 1000, 1001, 1010, ... (Sloane's A019513, Iacobescu 1997),

16. Sequences starting with terms which contain no three-term arithmetic progressions starting with: 1, 2, 4, 5, 10, 11, 13, 14, 28, ... (Sloane's A003278, Iacobescu 1997, Mudge 1997, Weisstein),

17. Numbers of the form : 2, 5, 37, 577, 14401, 518401, 25401601, 1625702401, 131681894401, ... (Sloane's A020549, Iacobescu 1997),

18. Numbers of the form : 2, 9, 217, 13825, 1728001, 373248001, 128024064001, ... (Sloane's A019514, Iacobescu 1997),

19. Numbers of the form : 2, 3, 13, 289, 34561, 24883201, 125411328001, 5056584744960001, ... (Sloane's A019515, Iacobescu 1997),

20. Sequences starting with terms which contain no three-term geometric progressions starting with: 1, 2, 3, 5, 6, 7, 8, 10, 11, 13, 14, 15, 16, ... (Sloane's A000452, Iacobescu 1997),

21. Numbers repeating the digit 1 times, where is the 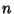th prime: 11, 111, 11111, 1111111, ... (Sloane's A031974, Iacobescu 1997). These are a subset of the Repunits,

22. Integers with all 2s, 3s, 5s, and 7s (prime digits) removed: 1, 4, 6, 8, 9, 10, 11, 1, 1, 14, 1, 16, 1, 18, 19, 0, ... (Sloane's A019516, Iacobescu 1997),

23. Integers with all 0s, 1s, 4s, and 9s (square digits) removed: 2, 3, 5, 6, 7, 8, 2, 3, 5, 6, 7, 8, 2, 2, 22, 23, ... (Sloane's A031976, Iacobescu 1997).

24. (Smarandache-Fibonacci triples) Integers 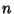such that , where is the SmarandacheFunction: 3, 11, 121, 4902, 26245, ... (Sloane's A015047; Aschbacher and Mudge 1995; Ibstedt 1997, pp. 19-23; Begay 1997).The largest known is 19,448,047,080,036,

25. (Smarandache-Radu triplets) Integers 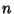such that there are no primes between the smaller and larger of and :224, 2057, 265225, ... (Sloane's A015048; Radu 1994/1995, Begay 1997, Ibstedt 1997). The largest known is 270,329,975,921,205,253,634,707,051,822,848,570,391,313,
26. (Smarandache crescendo sequence): Integers obtained by concatenating strings of the first integers for , 1, 2, ...:1, 1, 2, 1, 2, 3, 1, 2, 3, 4, ... (Sloane's A002260; Brown 1997, Brown and Castillo 1997). The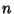th term is given by , where , with the Floor Function(Hamel 1997),

27. (Smarandache descrescendo sequence): Integers obtained by concatenating strings of the first 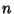integers for 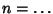, 2, 1:1, 2, 1, 3, 2, 1, 4, 3, 2, 1, ... (Sloane's A004736; Smarandache 1997, Brown 1997),

28. (Smarandache crescendo pyramidal sequence, a.k.a. Smarandache descrescendo symmetric sequence):Integers obtained by concatenating strings of rising and falling integers:1, 1, 2, 1, 1, 2, 3, 2, 1, 1, 2, 3, 4, 3, 2, 1, ... (Sloane's A004737; Brown 1997, Brown and Castillo 1997, Smarandache 1997),

29. (Smarandache descrescendo pyramidal sequence): Integers obtained by concatenating strings of falling and rising integers:1, 2, 1, 2, 3, 2, 1, 2, 3, 4, 3, 2, 1, 2, 3, 4, ... (Sloane's A004738; Brown 1997),

30. (Smarandache crescendo symmetric sequence): 1, 1, 1, 2, 2, 1, 1, 2, 3, 3, 2, 1, ... (Sloane's A004739, Brown 1997, Smarandache 1997),

31. (Smarandache permutation sequence): Numbers obtained by concatenating sequences of increasing length of increasing Odd Numbers and decreasing Even Numbers: 1, 2, 1, 3, 4, 2, 1, 3, 5, 6, 4, 2, ... (Sloane's A004741; Brown 1997, Brown and Castillo 1997),

32. (Smarandache pierced chain sequence): Numbers of the form for , 1, ...: 101, 1010101,10101010101, ... (Sloane's A031982; Ashbacher 1997). In addition, contains no Primes (Ashbacher1997),

33. (Smarandache symmetric sequence): 1, 11, 121, 1221, 12321, 123321, ... (Sloane's A007907; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 3; Mudge 1995),

34. (Smarandache square-digital sequence): square numbers all of whose digits are also squares: 1, 4, 9, 49, 100, 144, ... (Sloane's A019544; Mudge 1997),

35. (Square-digits): numbers composed of digits which are squares: 0, 1, 4, 9, 10, 11, 14, 19, 40, 41, ... (Sloane's A046030),

36. (Cube-digits): numbers composed of digits which are cubes: 1, 8, 10, 11, 18, 80, 81, 88, 100, 101, ... (Sloane's A046031),

37. (Smarandache cube-digital sequence): cube-digit numbers which are themselves cubes: 1, 8, 1000, 8000, 1000000, ... (Sloane's A019545; Mudge 1997),

38. (Prime-digits): numbers composed of digits which are primes: 2, 3, 5, 7, 22, 23, 25, 27, 32, 33, 35, ... (Sloane's A046034),

39. (Smarandache prime-digital sequence): prime-digit numbers which are themselves prime: 2, 3, 5, 7, 23, 37, 53, ... (Sloane's A019546; Smith 1996, Mudge 1997).

See also Addition Chain, Consecutive Number Sequences, Cubic Number, Euclid Number, EvenNumber, Fibonacci Number, Integer Sequence, Odd Number, Partition, Smarandache Function,Square Number


References

Aschbacher, C. Collection of Problems On Smarandache Notions. Vail, AZ: Erhus University Press, 1996.

Aschbacher, C. and Mudge, M. Personal Computer World. pp. 302, Oct. 1995.

Begay, A. ``Smarandache Ceil Functions.'' Bull. Pure Appl. Sci. 16E, 227-229, 1997.

Bencze, M. ``Smarandache Recurrence Type Sequences.'' Bull. Pure Appl. Sci. 16E, 231-236, 1997.

Bencze, M. and Tutescu, L. (Eds.). Some Notions and Questions in Number Theory, Vol. 2. http://www.gallup.unm.edu/~smarandache/SNAQINT2.TXT.

Brown, J. ``Crescendo & Descrescendo.'' In Richard Henry Wilde: An Anthology in Memoriam (1789-1847) (Ed. M. Myers). Bristol, IN: Bristol Banner Books, p. 19, 1997.

Brown, J. and Castillo, J. ``Problem 4619.'' School Sci. Math. 97, 221-222, 1997.

Dumitrescu, C. and Seleacu, V. (Ed.). Some Notions and Questions in Number Theory, 4th ed. Glendale, AZ: Erhus University Press, 1994. http://www.gallup.unm.edu/~smarandache/SNAQINT.TXT.

Dumitrescu, C. and Seleacu, V. (Ed.). Proceedings of the First International Conference on Smarandache Type Notions in Number Theory. Lupton, AZ: American Research Press, 1997.

Hamel, E. Solution to Problem 4619. School Sci. Math. 97, 221-222, 1997.

Iacobescu, F. ``Smarandache Partition Type and Other Sequences.'' Bull. Pure Appl. Sci. 16E, 237-240, 1997.

Ibstedt, H. Surfing on the Ocean of Numbers--A Few Smarandache Notions and Similar Topics. Lupton, AZ: Erhus University Press, 1997.

Kashihara, K. Comments and Topics on Smarandache Notions and Problems.ail, AZ: Erhus University Press, 1996.

Mudge, M. ``Top of the Class.'' Personal Computer World, 674-675, June 1995.

Mudge, M. ``Not Numerology but Numeralogy!'' Personal Computer World, 279-280, 1997.

Programs and the Abstracts of the First International Conference on Smarandache Notions in Number Theory. Craiova, Romania, Aug. 21-23, 1997.

Radu, I. M. Mathematical Spectrum 27, 43, 1994/1995.

Sloane, N. J. A. Sequences A000452, A000461, A000462, A001156/M0221, A002260, A003108/M0209, A003278/M0975, A004736, A004737, A004738, A004739, A004741, A007907, A008318, A008319, A008320, A0083201, A008322, A015047, A015048, A019524, A019511, A019513, A019514, A019515, A019516, A019523, A019544, A019545, A019546 A020549, A031974, A031976, A031980, A031981, A031982, A046030, A046031, and A046034 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html.

Smarandache, F. ``Properties of the Numbers.'' Tempe, AZ: Arizona State University Special Collection, 1975.

Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.

Smarandache, F. Collected Papers, Vol. 2. Kishinev, Moldova: Kishinev University Press, 1997.

Smith, S. ``A Set of Conjectures on Smarandache Sequences.'' Bull. Pure Appl. Sci. 15E, 101-107, 1996.
随便看

　

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。

　

Copyright © 2000-2023 Newdu.com.com All Rights Reserved
更新时间：2024/11/15 7:28:57