| 释义 |
Catalan's ConstantA constant which appears in estimates of combinatorial functions. It is usually denoted  , ,  , or , or 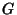 . It isnot known if . It isnot known if  is Irrational. Numerically, is Irrational. Numerically,
 | (1) |
 is [0, 1, 10, 1, 8, 1, 88, 4, 1, 1, ...](Sloane's A014538). is [0, 1, 10, 1, 8, 1, 88, 4, 1, 1, ...](Sloane's A014538).  can be givenanalytically by the following expressions, can be givenanalytically by the following expressions,
where 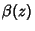 is the Dirichlet Beta Function. In terms of the Polygamma Function is the Dirichlet Beta Function. In terms of the Polygamma Function  , ,
Applying Convergence Improvement to (3) gives
 | (10) |
 is the Riemann Zeta Function and the identity is the Riemann Zeta Function and the identity
 | (11) |
 | (12) |
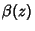 is the Dirichlet Beta Function. Glaisher (1913) gave is the Dirichlet Beta Function. Glaisher (1913) gave
 | (13) |
 | (14) |
 | (15) |
 is a Bernoulli Number and is a Bernoulli Number and 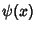 is a Polygamma Function (Finch). The Catalan constant mayalso be defined by is a Polygamma Function (Finch). The Catalan constant mayalso be defined by
 | (16) |
 (not to be confused with Catalan's constant itself, denoted (not to be confused with Catalan's constant itself, denoted  ) is a complete Elliptic Integral of theFirst Kind. ) is a complete Elliptic Integral of theFirst Kind.
 | (17) |
 | (18) |
 (in other words, (in other words,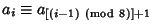 for for 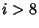 ) and ) and  is the Floor Function (Nielsen 1909).See also Dirichlet Beta Function is the Floor Function (Nielsen 1909).See also Dirichlet Beta Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 807-808, 1972.Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 551-552, 1985. Fee, G. J. ``Computation of Catalan's Constant using Ramanujan's Formula.'' ISAAC '90. Proc. Internat. Symp. Symbolic Algebraic Comp., Aug. 1990. Reading, MA: Addison-Wesley, 1990. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/catalan/catalan.html Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript. 1996. http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps. Glaisher, J. W. L. ``Numerical Values of the Series 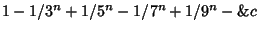 for for 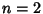 , 4, 6.'' Messenger Math. 42, 35-58, 1913. , 4, 6.'' Messenger Math. 42, 35-58, 1913. Gosper, R. W. ``A Calculus of Series Rearrangements.'' In Algorithms and Complexity: New Directions and Recent Results (Ed. J. F. Traub). New York: Academic Press, 1976. Nielsen, N. Der Eulersche Dilogarithms. Leipzig, Germany: Halle, pp. 105 and 151, 1909. Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computationof Constants.'' http://www.lacim.uqam.ca/pi/records.html. Sloane, N. J. A. SequencesA014538 andA006752/M4593in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. Srivastava, H. M. and Miller, E. A. ``A Simple Reducible Case of Double Hypergeometric Series involving Catalan's Constant and Riemann's Zeta Function.'' Int. J. Math. Educ. Sci. Technol. 21, 375-377, 1990. Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991. Yang, S. ``Some Properties of Catalan's Constant 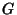 .'' Int. J. Math. Educ. Sci. Technol. 23, 549-556, 1992. .'' Int. J. Math. Educ. Sci. Technol. 23, 549-556, 1992.
|
![]() ,
, ![]() , or
, or ![]() . It isnot known if
. It isnot known if ![]() is Irrational. Numerically,
is Irrational. Numerically,









![]() for
for ![]() , 4, 6.'' Messenger Math. 42, 35-58, 1913.
, 4, 6.'' Messenger Math. 42, 35-58, 1913.![]() .'' Int. J. Math. Educ. Sci. Technol. 23, 549-556, 1992.
.'' Int. J. Math. Educ. Sci. Technol. 23, 549-556, 1992.