| 释义 |
Taylor SeriesA Taylor series is a series expansion of a Function about a point. A 1-D Taylor series is an expansion of aScalar Function 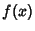 about a point about a point  . If . If  , the expansion is known as a Maclaurin Series. , the expansion is known as a Maclaurin Series.
 | (1) |
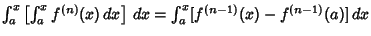 | |  | (2) |
Continuing,
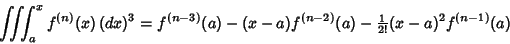 | (3) |
 | |  | (4) |
Therefore, we obtain the 1-D Taylor series | |  | (5) |
where  is a remainder term defined by is a remainder term defined by
 | (6) |
 , it must be true that , it must be true that
 | (7) |
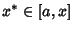 . Therefore, integrating . Therefore, integrating 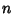 times gives the result times gives the result
 | (8) |
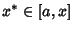 . .
An alternative form of the 1-D Taylor series may be obtained by letting
 | (9) |
 | (10) |
 | (11) |
A Taylor series of a Function in two variables 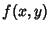 is given by is given by
This can be further generalized for a Function in 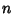 variables, variables,
 | (13) |
Rewriting,  | |  | | | (14) |
Taking  in (13) gives in (13) gives
Taking  in (14) gives in (14) gives  | |  | (16) |
or, in Vector form
 | (17) |
 | (18) |
 | (19) |
so the first few terms of the expansion are
 | (21) |
Taylor series can also be defined for functions of a Complex variable. By the Cauchy Integral Formula,
In the interior of  , ,
 | (23) |
 | (24) |
Using the Cauchy Integral Formula for derivatives,
 | (26) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 880, 1972.Arfken, G. ``Taylor's Expansion.'' §5.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 303-313, 1985. Morse, P. M. and Feshbach, H. ``Derivatives of Analytic Functions, Taylor and Laurent Series.'' §4.3 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 374-398, 1953.
|
![]() about a point
about a point ![]() . If
. If ![]() , the expansion is known as a Maclaurin Series.
, the expansion is known as a Maclaurin Series.

![]() is given by
is given by![]() variables,
variables,

![]() in (13) gives
in (13) gives
![]() in (14) gives
in (14) gives






