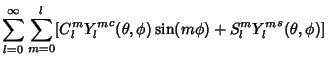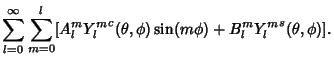| 释义 |
Correlation Coefficient--Gaussian Bivariate DistributionFor a Gaussian Bivariate Distribution, the distribution of correlation Coefficients is given by
where  is the population correlation Coefficient, is the population correlation Coefficient,  is a Hypergeometric Function, and is a Hypergeometric Function, and is the Gamma Function (Kenney and Keeping 1951, pp. 217-221). The Moments are is the Gamma Function (Kenney and Keeping 1951, pp. 217-221). The Moments are
where  . If the variates are uncorrelated, then . If the variates are uncorrelated, then  and and
so
But from the Legendre Duplication Formula,
 | (7) |
The uncorrelated case can be derived more simply by letting  be the true slope, so that be the true slope, so that  . Then . Then
 | (9) |
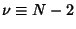 Degrees ofFreedom. Let the population regression Coefficient Degrees ofFreedom. Let the population regression Coefficient  be 0, then be 0, then  , so , so
 | (10) |
 | (11) |
 and using and using
gives
so
 | (14) |
 , where , where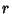 is the observed Coefficient, then is the observed Coefficient, then
Let 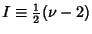 . For Even . For Even  , the exponent , the exponent  is an Integer so, by the Binomial Theorem, is an Integer so, by the Binomial Theorem,
 | (16) |
For Odd  , the integral is , the integral is
Let  so so  , then , then
But  is Odd, so is Odd, so  is Even. Therefore is Even. Therefore
Combining with the result from the Cosine Integral gives
 | (21) |
 | (22) |
 , then , then
 | (23) |
 | (24) |
If  , a skew distribution is obtained, but the variable , a skew distribution is obtained, but the variable  defined by defined by
 | (25) |
(Kenney and Keeping 1962, p. 266).
Let  be the slope of a best-fit line, then the multiple correlation Coefficient is be the slope of a best-fit line, then the multiple correlation Coefficient is
 | (28) |
 is the sample Variance. is the sample Variance.
On the surface of a Sphere,
 | (29) |
 is a differential Solid Angle.This definition guarantees that is a differential Solid Angle.This definition guarantees that  . If . If  and and  are expanded in Real Spherical Harmonics, are expanded in Real Spherical Harmonics,
Then
 | (32) |
where
 | (33) |
References
Bevington, P. R. Data Reduction and Error Analysis for the Physical Sciences. New York: McGraw-Hill, 1969.Eckhardt, D. H. ``Correlations Between Global Features of Terrestrial Fields.'' Math. Geology 16, 155-171, 1984. Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962. Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951. Pugh, E. M. and Winslow, G. H. The Analysis of Physical Measurements. Reading, MA: Addison-Wesley, 1966. |




![]() is the population correlation Coefficient,
is the population correlation Coefficient, ![]() is a Hypergeometric Function, and
is a Hypergeometric Function, and![]() is the Gamma Function (Kenney and Keeping 1951, pp. 217-221). The Moments are
is the Gamma Function (Kenney and Keeping 1951, pp. 217-221). The Moments are









![]() be the true slope, so that
be the true slope, so that ![]() . Then
. Then




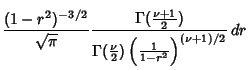

















![]() , a skew distribution is obtained, but the variable
, a skew distribution is obtained, but the variable ![]() defined by
defined by![]() be the slope of a best-fit line, then the multiple correlation Coefficient is
be the slope of a best-fit line, then the multiple correlation Coefficient is