Dedekind Eta Function

Let
| (1) |
 | (2) |
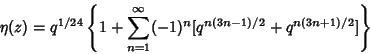 | (3) |
| (4) | |||
 | (5) |
(Weber 1902, p. 113; Atkin and Morain 1993).See also Dirichlet Eta Function, Theta Function, Weber Functions
References
Atkin, A. O. L. and Morain, F. ``Elliptic Curves and Primality Proving.'' Math. Comput. 61, 29-68, 1993. Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, 1902.
- Carlyle Circle
- Carmichael Condition
- Carmichael Function
- Carmichael Number
- Carmichael's Conjecture
- Carmichael Sequence
- Carmichael's Theorem
- Carmichael's Totient Function Conjecture
- Carnot's Polygon Theorem
- Carnot's Theorem
- Carotid-Kundalini Fractal
- Carotid-Kundalini Function
- Carry
- Carrying Capacity
- Cartan Matrix
- Cartan Relation
- Cartan Subgroup
- Cartan Torsion Coefficient
- Cartesian Coordinates
- Cartesian Ovals
- Cartesian Product
- Cartesian Trident
- Cartography
- Cascade
- Casey's Theorem