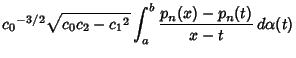| 释义 |
Orthogonal PolynomialsOrthogonal polynomials are classes of Polynomials 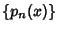 over a range over a range 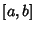 which obey anOrthogonality relation which obey anOrthogonality relation
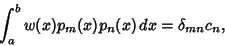 | (1) |
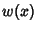 is a Weighting Function and is a Weighting Function and  is the Kronecker Delta. If is the Kronecker Delta. If  , then the Polynomialsare not only orthogonal, but orthonormal. , then the Polynomialsare not only orthogonal, but orthonormal.
Orthogonal polynomials have very useful properties in the solution of mathematical and physical problems. Just asFourier Series provide a convenient method of expanding a periodic function in a series of linearly independent terms,orthogonal polynomials provide a natural way to solve, expand, and interpret solutions to many types of importantDifferential Equations. Orthogonal polynomials are especially easy to generate usingGram-Schmidt Orthonormalization. Abramowitz and Stegun (1972, pp. 774-775) give a table of common orthogonalpolynomials.
| Type | Interval | 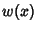 | 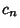 | | Chebyshev Polynomial of the First Kind | 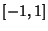 | 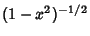 | 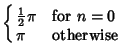 | | Chebyshev Polynomial of the Second Kind | 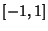 | 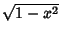 | 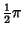 | | Hermite Polynomial |  |  |  | | Jacobi Polynomial |  | 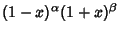 | 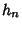 | | Laguerre Polynomial | 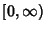 | 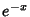 | 1 | | Laguerre Polynomial (Associated) | 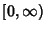 | 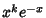 | 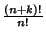 | | Legendre Polynomial | 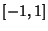 | 1 |  | | Ultraspherical Polynomial | 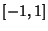 | 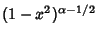 | 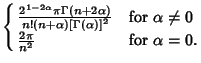 |
In the above table, the normalization constant is the value of
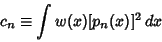 | (2) |
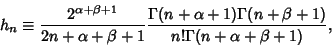 | (3) |
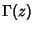 is a Gamma Function. is a Gamma Function.
The Roots of orthogonal polynomials possess many rather surprising and useful properties. For instance, let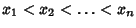 be the Roots of the be the Roots of the 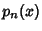 with with 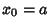 and and 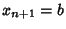 . Then each interval . Then each interval 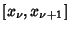 for for 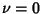 , 1, ..., , 1, ...,  contains exactly one Root of contains exactly one Root of 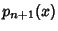 . Between two Roots of . Between two Roots of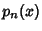 there is at least one Root of there is at least one Root of 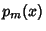 for for 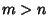 . .
Let 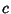 be an arbitrary Real constant, then the Polynomial be an arbitrary Real constant, then the Polynomial
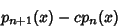 | (4) |
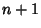 distinct Real Roots. If distinct Real Roots. If 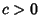 ( (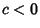 ), these Roots lie in the interior of ), these Roots lie in the interior of 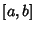 , with the exception of the greatest (least) Root which lies in , with the exception of the greatest (least) Root which lies in 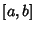 only for only for
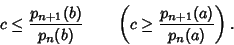 | (5) |
The following decomposition into partial fractions holds
 | (6) |
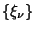 are the Roots of are the Roots of 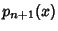 and and
Another interesting property is obtained by letting 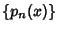 be the orthonormal set of Polynomialsassociated with the distribution be the orthonormal set of Polynomialsassociated with the distribution 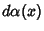 on on 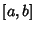 . Then the Convergents . Then the Convergents  of theContinued Fraction of theContinued Fraction
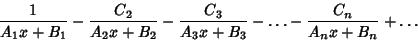 | (8) |
where  , 1, ...and , 1, ...and
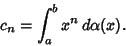 | (11) |
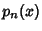 associated with the distribution associated with the distribution 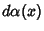 onthe interval onthe interval 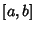 are Real and distinct and are located in the interior of the interval are Real and distinct and are located in the interior of the interval 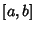 .See also Chebyshev Polynomial of the First Kind, Chebyshev Polynomial of the Second Kind, Gram-SchmidtOrthonormalization, Hermite Polynomial, Jacobi Polynomial, Krawtchouk Polynomial, LaguerrePolynomial, Legendre Polynomial, Orthogonal Functions, Spherical Harmonic, UltrasphericalPolynomial, Zernike Polynomial .See also Chebyshev Polynomial of the First Kind, Chebyshev Polynomial of the Second Kind, Gram-SchmidtOrthonormalization, Hermite Polynomial, Jacobi Polynomial, Krawtchouk Polynomial, LaguerrePolynomial, Legendre Polynomial, Orthogonal Functions, Spherical Harmonic, UltrasphericalPolynomial, Zernike Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.Arfken, G. ``Orthogonal Polynomials.'' Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 520-521, 1985. Iyanaga, S. and Kawada, Y. (Eds.). ``Systems of Orthogonal Functions.'' Appendix A, Table 20 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1477, 1980. Nikiforov, A. F.; Uvarov, V. B.; and Suslov, S. S. Classical Orthogonal Polynomials of a Discrete Variable. New York: Springer-Verlag, 1992. Sansone, G. Orthogonal Functions. New York: Dover, 1991. Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 44-47 and 54-55, 1975.
|
![]() over a range
over a range ![]() which obey anOrthogonality relation
which obey anOrthogonality relation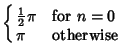
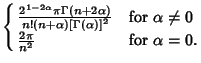
![]() be the Roots of the
be the Roots of the ![]() with
with ![]() and
and ![]() . Then each interval
. Then each interval ![]() for
for ![]() , 1, ...,
, 1, ..., ![]() contains exactly one Root of
contains exactly one Root of ![]() . Between two Roots of
. Between two Roots of![]() there is at least one Root of
there is at least one Root of ![]() for
for ![]() .
.![]() be an arbitrary Real constant, then the Polynomial
be an arbitrary Real constant, then the Polynomial

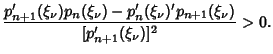
![]() be the orthonormal set of Polynomialsassociated with the distribution
be the orthonormal set of Polynomialsassociated with the distribution ![]() on
on ![]() . Then the Convergents
. Then the Convergents ![]() of theContinued Fraction
of theContinued Fraction