Division Algebra
A division algebra, also called a Division Ring or Skew Field, is a Ring in which every Nonzeroelement has a multiplicative inverse, but multiplication is not Commutative. Explicitly, a division algebra isa set together with two Binary Operators 
satisfying the following conditions:
- 1. Additive associativity: For all
, 
, - 2. Additive commutativity: For all
, 
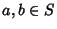, - 3. Additive identity: There exists an element
such that for all 
, 
, - 4. Additive inverse: For every there exists an element
such that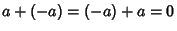 
, - 5. Multiplicative associativity: For all ,
, - 6. Multiplicative identity: There exists an element
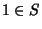not equal to 0 such that for all , 
, - 7. Multiplicative inverse: For every not equal to 0, there exists
, 
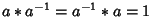, - 8. Left and right distributivity: For all ,
and 
.
is a Unit Ring for which 
is a Group. A division algebra mustcontain at least two elements. A Commutative division algebra is called a Field.In 1878 and 1880, Frobenius and Peirce proved that the only associative Real division algebras arereal numbers, Complex Numbers, and Quaternions. The Cayley Algebra isthe only Nonassociative Division Algebra. Hurwitz (1898) proved that theAlgebras of Real Numbers, Complex Numbers,Quaternions, and Cayley Numbers are the only ones where multiplication by unit``vectors'' is distance-preserving. Adams (1956) proved that 
-D vectors form an Algebra in which division (exceptby 0) is always possible only for 
, 2, 4, and 8.
References
Dickson, L. E. Algebras and Their Arithmetics. Chicago, IL: University of Chicago Press, 1923. Dixon, G. M. Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics. Dordrecht, Netherlands: Kluwer, 1994. Herstein, I. N. Topics in Algebra, 2nd ed. New York: Wiley, pp. 326-329, 1975. Hurwitz, A. ``Ueber die Composition der quadratischen Formen von beliebig vielen Variabeln.'' Nachr. Gesell. Wiss. Göttingen, Math.-Phys. Klasse, 309-316, 1898. Kurosh, A. G. General Algebra. New York: Chelsea, pp. 221-243, 1963. Petro, J. ``Real Division Algebras of Dimension 
contain 
.'' Amer. Math. Monthly 94, 445-449, 1987.
- Vector Potential
- Vector Quadruple Product
- Vector Space
- Vector Spherical Harmonic
- Vector Transformation Law
- Vector Triple Product
- Vee
- Velocity
- Venn Diagram
- Verging Construction
- Verhulst Model
- Veronese Surface
- Veronese Variety
- Versed Sine
- Versiera
- Versine
- Vertex Angle
- Vertex Coloring
- Vertex Connectivity
- Vertex Cover
- Vertex Degree
- Vertex Enumeration
- Vertex Figure
- Vertex (Graph)
- Vertex (Parabola)